Design and optimization of full decoupled micro/nano-positioning stage based on mathematical calculation

2.1 The concept design of lever amplifier

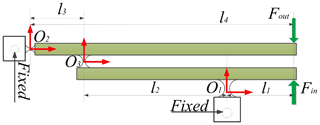
Lever amplifier based on flexure hinges possesses the advantages of high amplification ratio and simple structure (Choi et al., 2007). A two-stage amplifier is shown in Fig. 1.

Figure 1The two-stage amplifier.

Download

According to the mechanical principle, supposing that an outside force F_in is applied at free-end, the corresponding deformation displacement is δ. Therefore, output displacements d_out and δ_out are obtained. Considering Fig. 1, it can be observed that the two-stage amplifier is composed of two one-stage amplifiers. Assuming that the input displacement of two-stage magnifier is also δ, the total theoretical magnification ratio can be written by

For enhancing the input stiffness, the parallel structure is used as an amplification mechanism for amplifying the input displacement as shown in Fig. 2. The mechanism is fully symmetric along with the central line and is connected by two amplifiers in parallel. The symmetrical structure of input-end of the mechanism can protect the PZT from damage.

Figure 2Symmetrical structure with two 2-stage amplifiers.

Download

2.2 2-DOF positioning stage

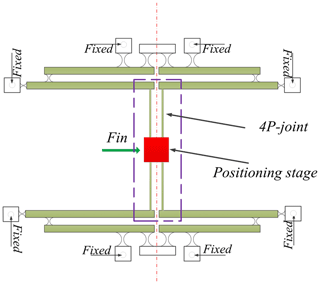
To eliminate cross coupling of the end-effector, symmetrical 1-DOF structure is shown in Fig. 3, where the double four-bar parallelogram mechanism is designed to connect the motion stage. The 4P-joint is composed of the four prismatic joints.

Figure 31-DOF symmetrical mechanism.

Download

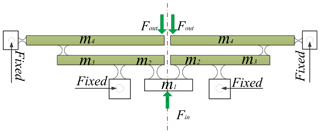
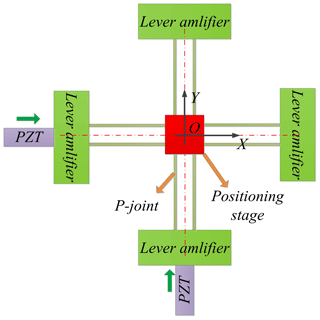
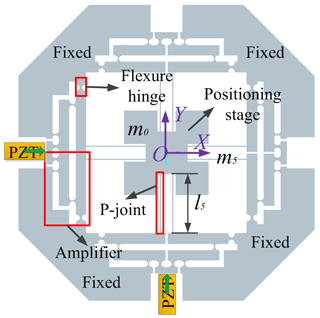
Simplified principle diagram of the 2-DOF positioning stage is presented as shown in Fig. 4, where the four mechanical displacement amplifiers and two double four-bar parallelogram mechanisms are utilized to design a fully symmetrical mechanism along with x- and y-directions. Particularly, the vertical distribution structure of two double four-bar mechanisms can effectively decrease cross coupling.

Figure 4Simplified principle diagram of mechanism.

Download

After a series of elaborated designs, three-dimension (3-D) model of the mechanism driven by PZT is proposed as shown in Fig. 5, input displacements of the motion platform, which are conducted by the PZTs installed in the x- and y-directions, can be magnified by the displacement amplifiers. Due to the symmetry of the structure and the four-bar parallelogram, parasitic motions of the positioning stage can be reduced or even eliminated. Circular hinges are adopted in the mechanical amplifier to avoid the parasitic motions.

Figure 5The 3-D diagram of the 2-DOF compliant mechanism.

Download

3.1 Amplification ratio and input stiffness analysis

Firstly, the amplification ratio and input stiffness of the mechanism are analyzed. The flexure circular notched hinge can be regarded as the general spring with bending stiffness (k_b) created by lateral force, torsion stiffness (k_t) caused by the torque and linear stiffness (k_l) produced by the axial force. Additionally, $k_{\mathrm{t}}^{\prime }$ and $k_{\mathrm{l}}^{\prime }$ are the torsion stiffness and linear stiffness of the prismatic beam (Koseki et al., 2002). Therefore, the rotational and linear deformations may simultaneously occur when a force is applied at the free-end of the beam. As shown in Fig. 6, the simplified diagrams of the circular notched hinge and prismatic beam are presented. Additionally, the torque M_t is produced after a small deformation angle Δθ occurs along with the center of the hinge from inside of the flexure hinge. Therefore, stiffness of different directions for flexure hinge can be represented in the following equations:

where E is the elastic modulus, b is the thickness of the flexure hinge, r and t are radius and smallest thickness of the circular notched hinge, a and l are the width and length of the prismatic beam, respectively.

Figure 6The flexure hinges: (a) the circular notched hinge; (b) the prismatic beam.

Download

Supposing that an input displacement δ_in is applied at the input-end of the mechanism, the corresponding input force and output displacement can be expressed by

where λ_AR and K_in are the amplification ratio and input stiffness of the micromanipulator, respectively.

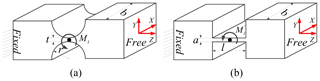
Due to the symmetry, only half of the amplifier mechanism is analyzed. According to the assumptions of literatures (Su and Yang, 2001a), force analysis simplified diagrams of the mechanical amplifiers are drawn up as shown in Fig. 7, where the Fig. 7b and c are two kinds of different one-stage amplifiers (Su and Yang, 2001b). Therefore, in consideration of the force and moment balance at the equilibrium state of the beam 2, the following equations can be derived as

where M_t and ${M_{\mathrm{t}}}^{\prime }$ are bending moments of the points O₂ and B. Additionally, the forces $F_{O_{\mathrm{2}}y}$ and $F_{B_y}$ can be calculated through multiplying stiffness by displacement. They are expressed by the following formulas

where $k_{O_{\mathrm{2}}y}$ and $k_{B_{\mathrm{l}}}$ are the lateral bending stiffness caused by force $F_{O_{\mathrm{2}}y}$ and output stiffness of the point B, respectively. $k_{O_{\mathrm{2}}\mathrm{t}}$ and $k_{B_{\mathrm{t}}}$ are the rotational stiffness of the points O₂ and B.

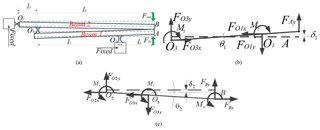
Figure 7Force diagram: (a) the deformation of the half of the amplifier; (b) forced diagram of beam 1; (c) Forced diagram of beam 2.

Download

Substituting Eqs. (7) and (8) into Eqs. (5) and (6), the θ₂ and δ₂ can be derived as

Therefore, the amplification ratio and input stiffness of the beam 2 can be calculated by the following equations

Then, substituting Eqs. (9) and (10) into Eqs. (11) and (12), following formulas can be obtained as

Similarly, considering the relationship of force and moment balance at the equilibrium state for the beam 1 as shown in Fig. 7b, the following formulas can be obtained by

where $k_{O_{\mathrm{1}}\mathrm{l}}$ and $k_{O_{\mathrm{1}}\mathrm{t}}$ are axial stiffness and rotational stiffness of the point O₁; $k_{O_{\mathrm{3}}\mathrm{t}}$ is rotational stiffness; k₂ is proposed as the stiffness of the series connection between the flexure hinge O₃ and the beam 2, which can be expressed by

where $k_{O_{\mathrm{3}}\mathrm{l}}$ is axial stiffness of the flexure hinge O₃. Combining the Eq. (15) into Eq. (18), the θ₁ and δ₁ can be calculated by

Therefore, according to the Fig. 7b, amplification ratio and input stiffness of the beam 1 can be represented by

Substituting Eqs. (19) and (20) into Eqs. (21) and (22), they can be rewritten by

Consequently, the total amplification ratio of the two-stage lever displacement mechanism is calculated by

Additionally, total input force can be obtained by $F_{\mathrm{in}}=\mathrm{2}{F}_{A_y}$, since the amplifier is symmetric and is connected in parallel. Therefore, input stiffness can also be calculated by

For calculating the values of k_in and λ_AR, the stiffness ($k_{B_{\mathrm{l}}}$) of the output point B must be firstly computed. According to the Fig. 4, it can be observed that the output stiffness of the micromanipulator is the stiffness of components except from the driven amplifier. Simplified diagrams of output components are shown in Fig. 8 when the platform is driven in y-directions. The marked signs, ${k_{\mathrm{l}}}^{\prime }$ and ${k_{\mathrm{t}}}^{\prime }$, are axial stiffness and rotational stiffness of the prismatic beam, respectively. And k₁ is the input stiffness of the two-stage amplifier when the input-end is at the point B and output-end is at the point A as shown in Fig. 7a.

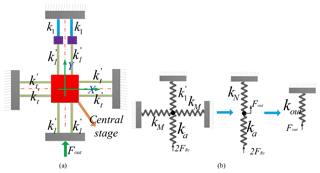
Figure 8The stiffness of output mechanism: (a) the diagram of the output mechanism; (b) the output stiffness transformation diagram.

Download

Output displacement of the mechanism, d_out, can be obtained when an input displacement d_in is applied at y-direction, whereas the amplifier of the x-direction will still hold since they have large transverse stiffness (Tang and Li, 2014). In addition, all rotational angles of the prismatic beams, (θ), are the same due to the identical structure. The potential energy stored in the flexible hinges can be derived as follows:

where α₁, β₁ and γ₁ are rotational angles of flexible hinges of the amplifier and can be written by

As shown in Fig. 8b, the stiffness k_N can be achieved by

According to the series-parallel relationship of the mechanism, the output stiffness k_out can be expressed by the following formula

where $M=\frac{\mathrm{1}}{l_{\mathrm{4}}^{\mathrm{2}}}+\frac{\mathrm{2}}{\mathrm{9}{l}_{\mathrm{2}}^{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{25}{l}_{\mathrm{1}}^{\mathrm{2}}}$, ${k_{\mathrm{t}}}^{\prime }$ and ${k_{\mathrm{l}}}^{\prime }$ are rotational stiffness and axial stiffness of the prismatic beam.

Because circular notched hinges and prismatic beams used in this study are identical, thus their stiffness can be expressed by

Due to the symmetry of the mechanism, the stiffness $k_{B_{\mathrm{l}}}$ can be obtained by

Combining the Eqs. (25) and (32), at the same time considering Eq. (2), total amplification ratio and input stiffness of the mechanism, which can be represented by the designed parameters including r, t, a, b and $l_i(i=\mathrm{1},\mathrm{\dots },\mathrm{5})$, are not provided here due to page limitations. To conveniently calculate the corresponding calculations, geometric parameters and properties of the material (AL7075-T6) of mechanism are listed in Table 1.

Table 1Geometric parameters (mm) and properties of material of the mechanism.

Download Print Version | Download XLSX

3.2 Reachable workspace analysis

For a 2-DOF motion platform, supposing that the AR_m is denoted as the amplification ratio of the mechanism and S is looked as the stroke of the PZT actuator, the workspace of the micromanipulation stage is represented by AR_mS×AR_mS. In this study, the bending stress only occurs on the cross section of flexible hinge when axial tension and shearing effects are not taken into consideration. Thus stress (σ_r) can be calculated as the following equation:

where σ_y and s>1 are the yield strength and the safety factor of the material. In addition, maximal stress ${\mathit{\sigma }}_r^{max}$ occurs when the angular displacement θ_max⁡ is maximum. It can be expressed using the following formula

where k_c and f(β) are the dimensionless concentration factor and compliance factor, respectively. They are expressed by (Smith, 2000).

where $\mathit{\beta }=t/\mathrm{2}r$ is the dimensionless geometry factor.

Assuming that the maximal input displacement is ${\mathit{\delta }}_{\mathrm{in}}^{max}$, corresponding to the output displacement of the motion stage is ${\mathit{\lambda }}_{\mathrm{AR}}{\mathit{\delta }}_{\mathrm{in}}^{max}$. According to the mechanical principle, the maximal stress may occur on the hinge O₃ connecting the two lever beams, since it not only suffers from the angular deformation created by output displacement, but may be also subjected to the angular deformation produced by the input displacement. Therefore, the maximal deformation angle can be derived by

Substituting Eqs. (37) into (34) and considering the Eqs. (36) and (33) at the same time, the maximal input displacement can be calculated as follows

Substituting values of the Table 1 into the Eq. (38) and letting the safety factor be 1.78. Maximal input displacement can be calculated as follows

Considering the amplification ratio of the mechanism, the output displacement of the stage can be 236.2 µm. Due to the symmetry of the mechanism, so the reachable workspace of the platform can be expressed as 236.2 µm × 236.2 µm.

Figure 9Deformations: (a) input at x direction and (b) input at y direction.

Download

3.3 Natural frequency analysis

To analyze free vibration of the 2-DOF micro positioning stage, the natural frequencies are achieved by utilizing Lagrange's method. The coordinate vector $\mathit{\eta }={\left[{\mathit{\eta }}_{\mathrm{1}},{\mathit{\eta }}_{\mathrm{2}}\right]}^T$ is used to describe the motions of x- and y-axes. The kinetic energy (T) and potential energy (V) stored in the mechanism can be expressed by the selected generalized coordinate and their derivations (Li et al., 2013). And then, substituting the kinetic and potential energies into the following Lagrange's equation

where $i=\mathrm{1},\mathrm{2}$, corresponds to the free vibration of x- and y-directions of the stage.

where the equivalent mass M=diag{M} and stiffness K=diag{k} are the 2×2 diagonal matrices, along with

where $m_i(i=\mathrm{0},\mathrm{1},\mathrm{\dots },\mathrm{5})$ are shown in the Figs. 2 and 5.

Solving the Eq. (41), the natural frequency of the stage can be obtained as

which has the unit of Hertz.

4.1 Model verification

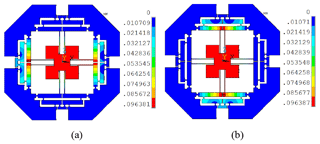
For analyzing the amplification ratio of the proposed mechanism, an input displacement with 20 µm is separately provided in the x- and y-directions and the deformation of the mechanism is shown in Fig. 9a and b, respectively. Therefore, the corresponding output displacements can be measured by selecting the points of the surface of the central platform and the average values of them are calculated with 87.58 and 87.57 µm. Additionally, the force can be also measured with 43.20 N. Therefore, the amplification ratio and input stiffness of the mechanism can be calculated as 4.38 and 2.16 N µm⁻¹, respectively.

Considering the workspace within the allowable maximum stress, the maximal input displacement of the Eq. (39) is simultaneously applied at the x- and y-directions. Thus, the maximal stress distribution and the corresponding displacement deformations are shown in Fig. 10. It can be seen that the maximal stress is 278.1 MPa at the point O₃, which is less than the allowable stress of the material. The Fig. 10b, c and d indicate the maximal output displacements of the whole mechanism. Based on the aforementioned analysis, the reachable workspace of the mechanism is measured with 215.50 µm × 215.50 µm.

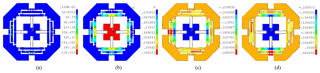
Figure 10The stress distribution and deformation diagrams: (a) maximal stress; (b) total output displacement; (c) output displacement at x-direction; (d) output displacement at y-direction.

Download

In order to analyze parasitic motion of the mechanism, the maximal input displacement is separately applied to the x- and y-axes. As shown in Fig. 11a and b, which is the output displacement of x-direction with 215.50 µm and parasitic motion at y-direction with 0.034 µm, respectively. Similarly, the Fig. 11c and d are the output displacement at y-direction with 215.50 µm and parasitic motion of x-direction with 0.036 µm. The parasitic motions of the x- and y-directions may be caused by the model errors and the deformations of the prismatic joint.

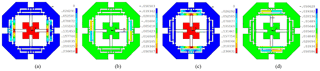
Figure 11Output displacements and parasitic motions: (a) output displacement at x-axis; (b) parasitic motion at y-direction; (c) output displacement at y-axis; (d) parasitic motion at x-direction.

Download

For verifying the dynamic model with the natural frequencies, the first four modal shapes of the structure are expressed in Fig. 12. The first modal shape is the rotational motion, which has the frequency with 179.99 Hz. The second and third modal shapes in the x- and y-directions are almost the same with values of 354.21 and 355.32 Hz, respectively. The fourth modal shape of the Z-direction is about 867.23 Hz.

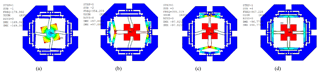
Figure 12The first four modal shapes of the mechanism: (a) the first modal shape; (b) the second modal shapes; (c) the third modal shape; (d) the fourth modal shape.

Download

Figure 13The verification of FEA: (a) deformation result; (b) stress distribution.

Download

Table 2Comparison results between calculated values and simulated values.

Download Print Version | Download XLSX

4.2 Discussions

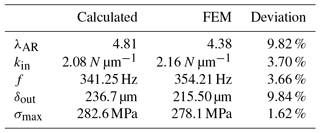
For further indicating the rationality of the design (Li and Wu, 2016), a comparison between the calculated values and the simulated values of FEA, in terms of amplification ratio, input stiffness, natural frequency, and maximum output displacement, is listed in Table 2. It can be observed that the maximal error is the output displacement and amplification ratio by using the benchmark of FEA. The reasons may be that the transverse deformation caused by the transverse force as shown in Fig. 7 is not taken into account in the calculated models and flexure hinge itself. In addition, the maximal stress is under the truly calculated value. The natural frequencies of the x- and y-directions are almost equivalent, which demonstrate that their performances are identical.

Cross coupling is the key performance of the 2-DOF micro-positioning stage. As shown in Fig. 11, the results of the maximum output displacements in two axes are listed in the Table 3. The output displacement of x-axis is 215.50 µm when input displacement is separately applied at x-direction, while the parasitic displacement of y-direction caused by x-direction is only 0.034 µm. Taking input displacement as the benchmark, coupling error of the y-axis is only for 0.1 %. Similarly, the parasitic motion of x-direction caused by y-direction is 0.036 µm with the output displacement is 215.50 µm at y-direction. Thus, coupling error on the x-axis is only for 0.1 % more than that of y-axis. Additionally, output displacements of x- and y-axes are up to 214.99 and 215.01 µm when the input displacements are simultaneously applied in the x- and y-directions. Based on the aforementioned analysis, the 2-DOF micromanipulation stage has low cross coupling and owns the best decoupling property.

Table 3Cross coupling in two axes.

Download Print Version | Download XLSX

5.1 Optimization problem description

Based on aforementioned equations, which reveal that the performances of the 2-DOF micro-positioning stage rely on the relative parameters. All established models mainly include these parametric variables: r, t, a, b, l₁, l₂, l₃, l₄, l₅, which influence the synthetical property of the stage.

For the mechanism with a special thickness (b=10 mm in this study), only eight parameters (r, t, a, l₁, l₂, l₃, l₄, l₅) need to be optimized. While other parameters can be determined by taking into account the length and width restrictions of the PZT with the addition of an appropriate assembling space. Otherwise, input stiffness of the mechanism should not surpass the minimum stiffness of the PZT. According to the geometrical relation of the structure, these variables should satisfy the following equation

With the selection of the amplification ratio of the stage as an objective function, the optimization process can be stated as follows:

• a.

  Maximum: Amplification ratio (λ_AR≥7).

• b.

  Variables to be optimized: r, t, a, l₁, l₂, l₃, l₄, and l₅.

• c.

  Subjecting to:

  • 1.

    Input stiffness value εk_in≤K_PZT;

  • 2.

    Natural frequency εf≥150 Hz;

  • 3.

    Theoretical amplification ratio AR≥7;

  • 4.

    Suffering from the restrictions of Eq. (45);

  • 5.

    The ranges of parameters:
    1.5 mm ≤ r≤2.0 mm, 0.3 mm ≤ t≤0.8 mm,
    0.3 mm ≤ a≤1 mm, 5 mm ≤ l₁≤15 mm,
    7 mm ≤ l₂≤20 mm, 5 mm ≤ l₃≤15 mm,
    20 mm ≤ l₄≤40 mm, 28 mm ≤ l₅≤40 mm.

Figure 14The experimental setup. (1) Host computer, (2) signal amplifier and controller, (3) compliant mechanism, (4) laser sensors, (5) laser collectors, (6) dSPACE controlling system, (7) DAQ board, (8) PZT actuators.

Download

5.2 Optimal results

The Genetic Algorithm (GA) is adopted in the current issue due to its superiority of fast convergence, fewer calculating time and higher robustness over other method such as simulated annealing algorithm (Mccall, 2005). The optimization process is implemented by the GA toolbox of the MATLAB software and the results of optimized parameters are: r=1.5 mm, t=0.78 mm, a=0.5 mm, l₁=5.47 mm, l₂=14.57 mm, l₃=7.90 mm, l₄=27.94 mm, l₅=28 mm, which will lead to an xy stage with λ_AR=7.87, k_in=13.39 N µm⁻¹ and the natural frequency f=367.07 Hz.

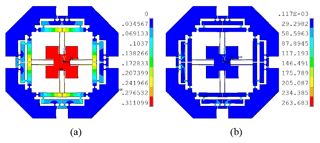
After optimization, simulation is carried out for demonstrating performances of the optimized micromanipulation stage. Maximum input displacements are applied at x- and y-axes and the total deflection and stress distribution of the mechanism are expressed in Fig. 13. It is observed that the output displacement of x-axis is 94.90 µm, and the corresponding input force is 214.63 N. Therefore, the optimized mechanism has an amplification ratio of 4.75 with an input stiffness of 10.63 N µm⁻¹. In addition, maximal stress is 263.68 MPa, which is far less than the yield strength of the material.

Furthermore, the first four natural frequencies are also analyzed and their values are 174.26, 348.31, 350.14 and 850.65 Hz, respectively. They are all less than the frequencies before optimizing and the frequencies of x- and y-directions are very close to the calculated values, which demonstrate that the structure optimization is effective.

6.1 Experimental setup

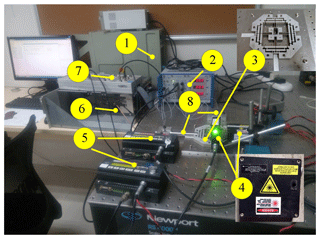
After fabricating, experimental setup of the micro-positioning stage is shown in Fig. 14. Two PZTs with stroke of 90 µm (model P-840.60 produced by Physik Instrumente, Inc.) are adopted to drive the micromanipulation stage, and the PZTs are actuated with a voltage of 0–100 V through a three-axis piezo-amplifier and driver (E-509 from the PI). Two laser displacement sensors and collectors (Microtrak II, head model: LTC-025-02, from MTI Instrument, Inc.) are used to measure the end-effector displacements of the two axes. The analog outputs of two sensors are connected to a PCI-based data acquisition (DAQ) board (PCI-6143 with 16-bit A/D convertors, from NI Corp.) through a shielded I/O connector block (SCB-68 from NI) with noise rejections. The digital outputs of the DAQ board are read by a host computer simultaneously.

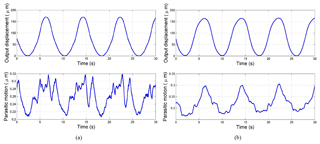
Figure 15The output displacements and parasitic motions: (a) the output displacement of x-axis and parasitic motion of y-axis; (b) the output displacement of y-axis and parasitic motion of x-axis.

Download

Since the sensitivity of the laser sensor is 2.0 mm/10 V and the maximum value of 16-bit digital signal corresponds to 10 V, the resolution of the displacement detecting system can be calculated as

However, due to a considerable level of the noise, the resolution of the sensor is claimed ±0.2 µm by the manufacturer. In the process of practical precision motion control experiments, it is found that the limitation of the fabricated prototype mainly arises from the laser displacement sensors which have a not-high resolution of ±0.2 µm.

6.2 Open test

To describe the dynamic properties of the proposed mechanism, the corresponding open-loop tests are carried out by using the dSPACE real-time simulation control system. As shown in Fig. 15a and b, which demonstrate respectively the output displacements and parasitic motions of x- and y-directions when the input voltage is $u=\mathrm{30}\sin (\frac{\mathit{\pi }}{\mathrm{4}}t-\frac{\mathit{\pi }}{\mathrm{2}})+\mathrm{30}$. The results indicate that the actual amplification ratio of the mechanical amplifier in x-direction by comparing the input and output displacements is about 3.51 and the parasitic motion for the y-direction is about 0.32 µm. While one of y-direction is calculated as 3.43 and the parasitic motion for the x-direction is only 0.31 µm. Based on the aforementioned tests, the experimental results are less than the analytical results. The main reasons may come from the assembly errors of the system and the preloaded force of the PZT. Additionally, parasitic motions of the x- and y-axes are very small, which can be ignored. Therefore, testing results demonstrate that the designed mechanism has excellent decoupled performance.

Figure 16The output displacements of x- and y-axes.

Download

To further illustrate the kinematic performance of the micro-positioning stage, the testing results of the x- and y-axes are shown in Fig. 16 when the two PZTs at x- and y-directions are driven simultaneously. The results indicate that the output displacements of x- and y-directions are not identical. The errors may be created by the preloaded force of PZTs and manufacturing defects between two axes.

6.3 Tracking experiments

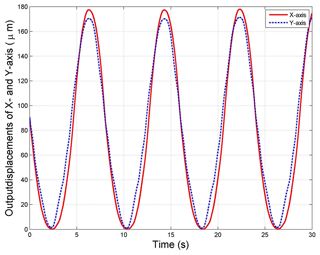
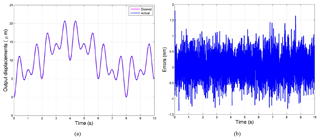
For further validating the performances of micro/nano-positioning platform, a robust tracking controller is used to obtain the well tracking effect. The reference input displacement is the signal with different frequencies since the hysteresis phenomenon of piezoelectric actuator is a rate-dependent hysteresis. Therefore, the robust controller can effectively eliminate the drawback caused by rate-dependent of the PZT-actuated micromanipulator. The tracking results and corresponding errors is shown in Fig. 17, where output displacement is well tracking with the input displacement and the error is low than 0.01 %. Thus the optimal design is suitable for this compliant mechanism.

Table 4Property comparisons for proposed xy stages.

Download Print Version | Download XLSX

Figure 17The tracking result and error: (a) the tracking result; (b) the tracking error.

Download

6.4 Discussions

From the Figs. 15 and 16, we can see that the output displacements of the x- and y-axes are not exactly same, the main reasons maybe come from the errors coming from installation and manufacturing. Thus, the rotation of end-effector can exist, but it may be minor affections for the other orientation.

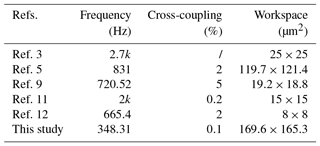
Based on aforementioned modeling, analyzing, and testing, the results demonstrate that the proposed 2-DOF micro-positioning stage with mechanical amplifier owns some advantages, in terms of large motion, and low cross coupling. A comparison with other proposed 2-DOF stages are completed in Table 4. The natural frequencies of the presented stages in Ref. 3 and Ref. 11 are higher than other mechanisms, but their working ranges are very small, which seriously limit their further applications. Additionally, the performances in terms of cross coupling and workspace of the other two stages presented in Ref. 5, Ref. 9 and Ref. 12 are obviously lower than the proposed in this study.