the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Posture adjustment of workpiece based on stepwise matching by self-adaptive differential evolution algorithm
Lei Jiang
Yong Li
Yisheng Zou
Kun Tang
Yulong Fu
Shuwen Ma
The workpiece contour errors from previous process affect current and subsequent process. In order to improve the uniformity of workpiece allowance distribution, a stepwise workpiece matching adjustment method with contact inspection is developed. This method includes two stepwise registration processes. At first, some pairs of measured points on the theoretical and actual surfaces are selected to build the corresponding local coordinate systems, and then the rough matching matrixes are obtained by the coordinate systems alignment. During the fine matching process, the objective function based on the least square method is established by the measured point sets adjusted through the rough matching. The fine matching matrixes can be obtained by self-adaptive differential evolution algorithm. The posture adjustment can be realized by transforming coordinate systems of 5 axis machine tool, of which adjusted values can be calculated by the matching matrixes and the machine tool topology. At last, some experiments were presented to demonstrate the performance of the method.
The uniform allowance distribution is very important for ensuring machining accuracy. In machining process, due to multi-clamping, machining distortion, the geometrical errors of machining tool and so on, these factors may lead to non-uniform allowance distribution (overcut or undercut) of some surfaces in current process even if the shape of the workpiece meets the design requirements. This will result in the machining quality of the current and subsequent process being seriously affected.
Recently, with the development of inspection technologies and instruments, it is necessary to apply inspection technologies and instruments, such as on-machine probing system, contact scanning system, non-touch 3-D scanning system, coordinate measuring machine (CMM), coordinate measuring arm (CMR), to inspect workpiece contour deviation between processes.
After inspection, how to improve allowance uniformity for the current process is put forward. Some efforts have been made concerning workpiece posture adjustment method. The solutions include adjusting workpiece localization, relocating workpiece by adaptive fixture, regenerating NC program, etc. With the development of machine tool and NC control technology, the swivel, frames and inclined plane machining functions of 5 axis machine tool can be used to control rotary axis and angle the tool (transform workpiece coordinate system) (HEIDENHAIN, 2011; SINUMERIK, 2009). Comparing with other methods, workpiece posture adjustment can be realized easily by workpiece matching and WCS transformation.
There are different matching methods for non-contact (optical) and contact inspection. For non-contact inspection, the most widely used point set matching method is based on the iterative closest point (ICP) algorithm (Maiseli et al., 2017). Recent years, some scholars have developed improved ICP algorithm and applied them to point cloud matching (Du et al., 2016; Maier-Hein et al., 2012). Ge and Thomas (2016) proposed the nonlinear Gauss-Helmert-least square (GH-LS) approach for 3-D point cloud. Ma et al. (2017) proposed an efficient rotation estimation algorithm for point clouds of structured scenes. Zhu et al. (2014) presented a unified frame work for best-fitting of a complex rigid surface. Tang et al. (2016) presented a locating error analysis approach for workpiece with general fixture layouts and parameterized tolerances. Srinivasan et al. (2015) developed automatic part localization in a CNC machine coordinate system by means of 3-D scans. Most of the matching methods mentioned above require the corresponding surface equations or surface properties which are very difficult to be obtained, especial irregular surfaces. These lead the non-contact inspection and point set matching methods only to work with roughly pre-registered surfaces (Zhang et al., 2009; Evgeny et al., 2006; Sun et al., 2009; Tan et al., 2014).
Comparing with non-contact inspection, contact inspection has more relationship information: theoretical and actual measured point pairs with definite detection directions, point sets, tolerances and corresponding surfaces. For contact inspection, some researchers modeled the matching as a constrained least squares optimization problem. Yan et al. (2004) applied genetic algorithms (GA) to solve the problem of stock surface matching. Wang et al. (2015) improved the allowance distribution of blade by multivariate statistical process control. Mehrad et al. (2014) realized the matching between point sets and design model through rough and fine localizations, which is based on similarities in curvatures and distances. A combination of the alternating optimization and successive linearization methods was proposed by Dai et al. (2010). However, the constrained optimization is difficult to solve in view of the numerical stability, efficiency and accuracy (Tan et al., 2014).
In this paper, a new matching method is developed for the posture adjustment of workpiece with contact inspection. The method includes two stepwise matching processes, and the optimal rotation and translation adjustment of the actual measured point set relative to the theoretical measured point set can be obtained by the coordinate systems alignment and self-adaptive differential evolution (SADE) algorithm.
This paper is structured as follows: in Sect. 2, a proposed workpiece posture matching method is described in detail; in Sect. 3, a method for calculating adjustment values of machine tool is introduced, and an application and comparison example is presented in Sect. 4; Sect. 5 is a conclusion of this paper.
The workpiece posture adjustment is an effective and direct method to achieve the accurate localization and unify the allowance distribution. The most essential issue is to achieve the matching between the workpiece actual and theoretical location. Namely, it is necessary to search for the optimal Euclidean transformation through the measured data.
Set the inspection coordinate system (ICS) as the workpiece coordinate system (WCS). Define the actual measured point set as , the corresponding theoretical measured point set as , the number of measured points as n, the tolerance of workpiece surface as ε.
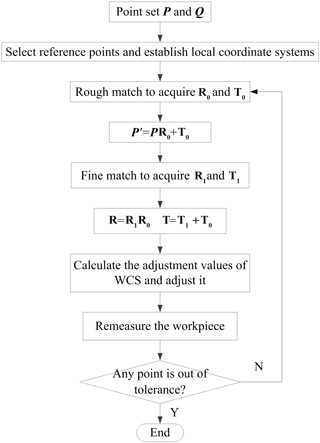
The proposed procedure including rough and fine matching, which can be expressed as following:
Step 1. Select 3 pairs of corresponding points as the reference points in the P and Q point sets respectively, and establish actual and theoretical local coordinate systems;
Step 2. Rough matching is achieved by local coordinate systems alignment, and the rough matching matrixes R0 and T0 are calculated by the coordinate systems alignment;
Step 3. Actual point set P is translated into P′ through the rough matching matrixes;
Step 4. The SADE algorithm is adopted to search for the fine matching matrixes R1 and T1 of P′ relative to Q;
Step 5. Calculate the total transformation matrixes R and T from R0, R1, T0 and T1;
Step 6. Calculate the adjustment values of WCS and adjust it;
Step 7. Remeasure the workpiece, and if it does not exist overcut or undercut, end the matching process; else, return to step 2.
2.1 The construction of the local coordinate systems
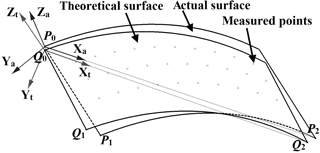
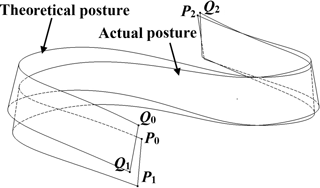
As shown in Fig. 2, the posture errors exist between the theoretical and the actual surfaces. In order to establish the local coordinate systems, 3 pairs of measured points on the theoretical surface and the actual surface are respectively selected as the reference points. In general, the points are non-collinear, and they should be distributed on the measured surface as far as possible outside the other points, such as corner point and so on. According to the reference points, the unit axis vectors of the local coordinate systems can be calculated.
The theoretical and actual local coordinate systems are defined as Q0−XtYtZt and P0−XaYaZa respectively. Define the axial vectors of actual local coordinate systems as ia, ja and ka, P0 as the origin; define the axial vectors of theoretical coordinate systems as it, jt and kt, Q0 as the origin. Then
2.2 The solution of the rough matching matrixes
The rough matching is completed through the alignment between the local coordinate systems. After the rough matching, P0−XaYaZa can coincide with Q0−XtYtZt completely. The relation between local coordinate systems and the rotation matrix R0 is expressed as Eq. (4) (Yan et al., 2004).
Where the α0, β0, γ0 represent the orientation angle from P0−XaYaZa and Q0−XtYtZt respectively, which can be expressed in Eq. (5).
Where R0(i,j) (, 2, 3) represents the value of the ith row and the jth column of the matrix R0.
The points P0 and Q0 are the centroid of the point set P and Q respectively, and the translation matrix can be acquired by Eq. (6).
The rough posture errors between the theoretical and the actual surfaces can be described by the rough posture error matrix PE0 in Eq. (7).
2.3 The solution of the fine matching matrixes
Define the fine matching rotation matrix as R1 (its form is similar to R), and the translation matrix as T1 (its form is similar to T). According to the similar definition, the fine matching matrixes parameters includes the orientation angles α1, β1, γ1 and the translation values tx1, ty1, tz1.
2.3.1 The objective function
After the rough matching, actual measured point set P is converted to P′, which is denoted as . The fine matching is to search for the optimal transformation R1 and T1, and make the point set P′ be close to Q in the range of tolerance. Generally, the matching result is evaluated by the distance between the point set Q and P′. So the fine matching can be summed up as a minimization problem, and its objective function can be defined as Eq. (8).
From Eq. (8), it is obvious that the objective function belongs to nonlinear problem. In order to improve the computational efficiency, it is necessary to reduce the dimension of the objective function. According to Eq. (6), the Eq. (8) can be expressed as follows
Then the objective function can be defined to search the optimal orientation angles to minimize f(R1).
2.3.2 Optimization operation
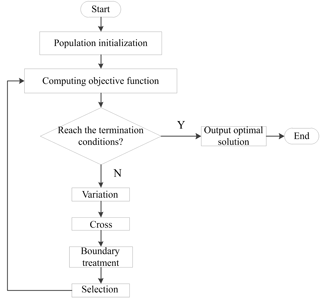
In this paper, the objective function can be solved by the SADE algorithm, which is developed based on the basic differential evolution algorithm. The difference between them is the self-adaptive variation operator and crossover operator can be designed in the SADE algorithm. Therefore, it can not only avoid low search efficiency and poor global optimal solutions caused by the overlarge variation rate, but also avoid the low population diversity and prematurity caused by the too small variation rate (Tasoulis et al., 2004). Figure 3 is the procedure of the SADE algorithm.
The self-adaptive variation operator F can be defined in Eq. (10), which controls the amplification of deviation variables (Tasoulis et al., 2004; Storn and Price, 1997).
Where F0 is the initial variation operator, Gm is the maximum evolution generation, and G represents the current evolution generation.
At the start of computation process, set G=1 and F=2F0. F is large which can keep the individuals diversity and avoid the prematurity. As the process progresses, F is gradually decreased which is close to F0 at the end. It will increase the probability of searching for the global optimal solutions.
The self-adaptive crossover operator CR can be defined in Eq. (11),
where CRmin is the minimum crossover operator and CRmax represents the maximum one.
Generally, the larger the value of CR is, the more prone cross. When CR is small, it can maintain the diversity of the population and global search. According to Eq. (11), CR gradually increases as G increases. Therefore, at the beginning of the computation process, population diversity can be better guaranteed and global search can be performed. Then, the local search ability can be enhanced to improve the accuracy of the algorithm.
Through the rough matching, the posture error between theoretical and actual surface is decreased greatly. Theoretically, the ranges of α1, β1 and γ1 cannot exceed the corresponding value of α0, β0 and γ0, i.e., the rough matching determines the boundary values of the subsequent optimization variables approximately. By taking into account the rough matching error, their ranges can be enlarged appropriately. Therefore, the ranges of α1, β1 and γ1 can be defined as [, α0+k1], [, β0+k2] and [, γ0+k3] respectively, where ki (i=1, 2, 3) are constants.
Through the matrixes R and T, according to the structure type of the 5 axis machine tools, the adjustment values can be solved, including rotation angles and translation values of each axis. With swivel, frame or inclined plane machining functions, the localization of WCS is defined by some specific feed axis movement (HEIDENHAIN, 2011; SINUMERIK, 2009). They can be calculated by the matching matrixes and topology of machine tool.
The WCS translation can be realized by the movement values SX, SY, SZ of x, y and z axis. In addition, the WCS orientation can be defined by the rotation of rotary axis. Taking 5 axis machine tool of XFYZBA topology (which has two rotary axes in the head) as an example, the orientation can be defined by the rotation angles SA, SB of a and b axis.
Taking worktable as reference, the WCS origin point and orientation can be described by integrated geometric model of 5 axis machine tools, registration matrix T and R. The adjustment values can be deduced as following, which is based on the inverse kinematical transformation theory (Zhu et al., 2012):
where (0, 0, LAB) are the a axis origin coordinates in the b axis coordinates system, (LX, LY, LZ) are the cutter location point coordinates in the a axis coordinates system.
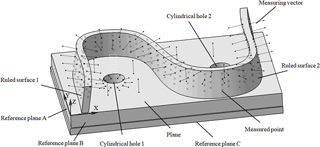
Because the accuracy of aviation structural part is susceptible to the machining process complexity and error factors, the need for machining localization adjustment is more urgent. As representative of typical aviation structure part, an S shape test piece from ISO test conditions for machining centers was applied to verify the proposed method (ISO CD 10791-7, 2017). It includes one plane, two cylindrical holes and two ruled surfaces, whose machining tolerances are ±0.035 mm, and the WCS is defined by reference planes A, B and C, as shown in Fig. 4. The initial posture of the machined surface is shown in Fig. 5. All the measured points (40 points) are overcut or undercut, and the average over tolerance is about 1.8797 mm.
4.1 The rough matching
Firstly, the machined surface of the workpiece is measured to acquire the theoretical measured point set Q. Then 3 pairs of reference points are selected to establish the local coordinate systems, as shown in Table 1, and the rough matching matrixes are shown in Table 2.
4.2 The fine matching
After the rough matching, the approximate boundary values can be determined based on PE0 as , , .
According to the objective function and the optimization variables, relevant parameters of the SADE algorithm are determined. The reasonable value of NP is selected between 5D and 10D (NP is the population size and D is the dimension of the variable), and a good initial value of variation operator F is between 0.5 and 0.8 (Storn and Price, 1997).In this paper, D is 3, and NP is 30, so the initial variation operator F0 can be selected between 0.25 and 0.4. Gm is generally in the range of 100 to 500 (Tasoulis et al., 2004).
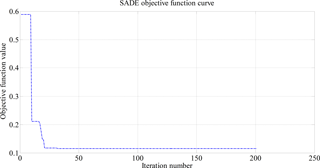
Figure 6 is the optimization curve of SADE algorithm. After 200 iterations, the global optimal solutions can be obtained (, , , f(R1)=0.1148 mm). The fine matching matrixes R1 and T1 are shown in Table 3.
4.3 The adjustment of the machine tool
The final rotational and translational transformation matrixes R and T can be solved by Eq. (2). The adjustment values of the machine tool are listed in Table 4. According to the values, the workpiece posture is adjusted with WCS.
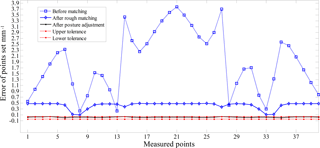
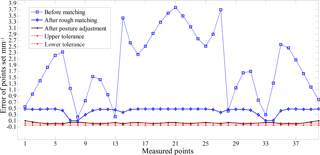
Figure 7 shows the error distribution of measured points which represent before the matching, after rough matching and posture adjustment. Comparing PE1 with PE0, it is obvious that the error between the theoretical and actual posture is decreased greatly. Through posture adjustment, none of the measured points is out of tolerance.
In order to verify the effectiveness of the method proposed, a comparison with other localization algorithm is conducted. The algorithm consists of rough surface matching and accuracy surface matching, and genetic algorithm-simplex (GAs) are introduced in the step of accuracy surface matching (Yan et al., 2004).
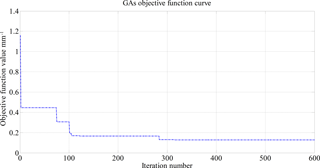
Figure 8 is the optimization curve of GAs. The global optimal solutions are obtained after 600 iterations (, , , f(R1)=0.12812 mm). Figure 9 is the error distribution of measured points after posture adjustment by GAs, and there are 10 measured points which are still over tolerance.
Comparing with the method proposed in this study, the computation speed and the effect of posture adjustment by GAs is not very good.
In order to solve the problem about non-uniform allowance distribution in precise machining process, this paper develops a stepwise matching method based on contact measured point sets for workpiece posture adjustment. The stepwise matching includes the rough and fine matching processes. After matching, the spatial transformation matrixes R, T and the adjustment values of machine tool can be obtained accurately. At last, some experiments were presented to demonstrate the performance of the method.
Data can be made available upon reasonable request. Please contact Lei Jiang (jianglei0506@163.com).
| Q | Theoretical point set |
| P | Actual point set |
| ia, ja, ka | Axial vectors of actual coordinate system |
| it, jt, kt | Axial vectors of theoretical coordinate system |
| P′ | Actual point set after rough matching |
| Actual point set after fine matching | |
| R0 | Rough matching rotation matrix |
| T0 | Rough matching rotation matrix |
| R1 | Fine matching rotation matrix |
| T1 | Fine matching translation matrix |
| R | Final rotation matrix |
| T | Final translation matrix |
| PE0 | Rough posture error matrix |
| PE1 | Adjusted posture error matrix |
LJ and YL designed the experiments. KT and YF carried the experiments out. YL developed the model code and performed the simulations. LJ prepared the manuscript with contributions from all co-authors. YZ and SM revised the manuscript.
The authors declare that they have no conflict of interest.
This work is supported by the Special Fund of
High-end CNC Machine Tools and Basic Manufacturing Equipment
(2015ZX04001002), China.
Edited by: Lotfi Romdhane
Reviewed by: two anonymous referees
Dai, Y., Chen, S., Kang, N., and Li, S.: Error calculation for corrective machining with allowance requirements, Int. J. Adv. Manuf. Tech., 49, 635–641, https://doi.org/10.1007/s00170-009-2437-5, 2010.
Du, S., Liu, J., Bi, B., Zhu, J., and Xue, J.: New iterative closest point algorithm for isotropic scaling registration of point sets with noise, J. Vis. Commun. Image R., 38, 207–216, https://doi.org/10.1016/j.jvcir.2016.02.019, 2016.
Evgeny, L., Dmitry, C., and Aniko, E.: Pre-registration of arbitrarily oriented 3D surfaces using a genetic algorithm, Pattern Recogn. Lett., 27, 1201–1208, https://doi.org/10.1016/j.patrec.2005.07.018, 2006.
Ge, X. M. and Thomas, W.: Surface-based matching of 3D point clouds with variable coordinates in source and target system, ISPRS J. Photogramm., 111, 1–12, https://doi.org/10.1016/j.isprsjprs.2015.11.001, 2016.
HEIDENHAIN: iTNC 530 operation Manual V6, vol. 12, HEIDENHAIN, Traunreut, Germany, 2011.
ISO CD 10791-7: Test conditions for machining centres-Part 7: Accuracy of finished test piece, ISO CD 10791-7, International Organization for Standardization (ISO), Geneva, Switzerland, 2017.
Ma, Y., Guo, Y., Lei, Y., Lu, M., and Zhang, J.: Efficient rotation estimation for 3D registration and global localization in structured point clouds, Image Vision Comput., 67, 52–66, https://doi.org/10.1016/j.imavis.2017.09.003, 2017.
Maier-Hein, L., Franz, A. M., Santos, T. R. D., Schmidt, M., Fangerau, M., and Meinzer, H. P.: Convergent iterative closest-point algorithm to accommodate anisotropic and in homogenous localization error, IEEE T. Pattern Anal., 34, 1520–1532, https://doi.org/10.1109/tpami.2011.248, 2012.
Maiseli, B., Gu, Y., and Gao, H.: Recent developments and trends in point set registration methods, J. Vis. Commun. Image R., 46, 95–106, https://doi.org/10.1016/j.jvcir.2017.03.012, 2017.
Mehrad, V., Xue, D., and Gu, P.: Robust localization to align measured points on the manufactured surface with design surface for freeform surface inspection, Comput. Aided Design, 53, 90–103, https://doi.org/10.1016/j.cad.2014.04.003, 2014.
SINUMERIK: 5-axis machining Manual, vol. 05, SINUMERIK, Erlangen, Germany, 2009.
Srinivasan, H., Harrysson, O. L. A., and Wysk, R. A.: Automatic part localization in a CNC machine coordinate system by means of 3D scans, Int. J. Adv. Manuf. Tech., 81, 1127–1138, https://doi.org/10.1007/s00170-015-7178-z, 2015.
Storn, R. and Price, K.: Differential Evolution-A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces, J. Global Optim., 11, 341–359, 1997.
Sun, Y., Wang, X., Guo, D., and Jian, L.: Machining localization and quality evaluation of parts with sculptured surfaces using SQP method, Int. J. Adv. Manuf. Tech., 42, 1131–1139, https://doi.org/10.1007/s00170-008-1673-4, 2009.
Tan, G., Zhang, L., Liu, S., and Ye, N.: An unconstrained approach to blank localization with allowance assurance for machining complex parts, Int. J. Adv. Manuf. Tech., 73, 647–658, https://doi.org/10.1007/s00170-014-5798-3, 2014.
Tang, W., Li, Y., Yu, J., Zhang, J., and Yu, L.: Locating error analysis for workpieces with general fixture layouts and parameterized tolerances, P. I. Mech. Eng. B-J. Eng., 230, 416–427, https://doi.org/10.1177/0954405414551075, 2016.
Tasoulis, D. K., Pavlidis, N. G., and Plagianakos, V. P., and Vrahatis, M. N.: Parallel Differential Evolution, Evol. Comput., 2, 2023–2029, https://doi.org/10.1109/cec.2004.1331145, 2004.
Wang, P., Li, S., Zhang, D., and Li, Y.: The machining error control of blade shape based on multivariate statistical process control, P. I. Mech. Eng. B-J. Eng., 229, 1912–1924, https://doi.org/10.1177/0954405414540648, 2015.
Yan, S. J., Zhang, Y. F., Peng, F. Y., and Lei, X. D.: Research on the localization of the workpieces with large sculptured surfaces in NC machining, Int. J. Adv. Manuf. Tech., 23, 429–435, https://doi.org/10.1007/s00170-003-1897-2, 2004.
Zhang, D. H., Zhang, Y., and Wu, B. H.: Research on the adaptive machining technology of blisk, Adv. Mat. Res., 69–70, 446–450, https://doi.org/10.4028/www.scientific.net/amr.69-70.446, 2009.
Zhu, L. M., Xiong, Z. H., Ding, H., and Xiong, Y. L.: A distance function based approach for localization and profile error evaluation of complex surface, J. Manuf. Sci. E.-T. ASME, 126, 542–554, https://doi.org/10.1115/1.1763186, 2014.
Zhu, S. W., Ding, G. F., Qing, S., Jiang, L., Li, Z., and Yan, K. Y.: Integrated geometric error modeling, identification and compensation of CNC machine tools, Int. J. Machine Tools Manufacture, 52, 24–29, https://doi.org/10.1016/j.ijmachtools.2011.08.011, 2012.