the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
Structural integrity investigation for RPV with various cooling water levels under pressurized melting pool
Jianfeng Mao
Yunkai Liu
Shiyi Bao
Lijia Luo
Zhiming Lu
Zengliang Gao
The strategy denoted as “in-vessel retention (IVR)” is widely used in severe accident (SA) management by most advanced nuclear power plants. The essence of IVR mitigation is to provide long-term external water cooling in maintaining the reactor pressure vessel (RPV) integrity. Actually, the traditional IVR concept assumed that RPV was fully submerged into the water flooding, and the melting pool was depressurized during the SA. The above assumptions weren't seriously challenged until the occurrence of Fukushima accident on 2011, suggesting the structural behavior had not been appropriately assessed. Therefore, the paper tries to address the structure-related issue on determining whether RPV safety can be maintained or not with the effect of various water levels and internal pressures created from core meltdown accident. In achieving it, the RPV structural behaviors are numerically investigated in terms of several field parameters, such as temperature, deformation, stress, plastic strain, creep strain, and total damage. Due to the presence of high temperature melt on the inside and water cooling on the outside, the RPV failure is governed by the failure mechanisms of creep, thermal-plasticity and plasticity. The creep and plastic damages are interacted with each other, which further accelerate the failure process. Through detailed investigation, it is found that the internal pressure as well as water levels plays an important role in determining the RPV failure time, mode and site.
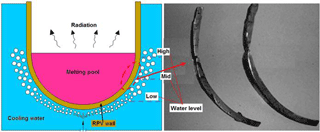
During the severe accident (SA) causing a pressurized core meltdown, the reactor pressure vessel (RPV) integrity may be threatened by various thermal-mechanical loadings. In the accident event, a large quantity of liquid corium can relocated to the lower head (LH) of RPV. Without proper external cooling, the local overheating must lead to the LH breach, resulting in the release of a large amount of core material into the containment (see Fig. 1). In overcoming it, the famous strategy of “In-vessel retention (IVR)” based on the idea of external water cooling is widely used by most advanced nuclear power plant (NPP) (Yue et al., 2015). Moreover, the so called “IVR” mitigation had been certified by the authority organization as a standard measure for preventing overheating of the core in severe accident since 1996 (Schulz et al., 2006). Essentially, the IVR mitigation is to provide long-term water cooling on the outer RPV wall, so the decay heat is able to be removed without any active actions and assistance measures (Jung et al., 2015). In the traditional concept of IVR, there are two assumptions (S.-H. Kim et al., 2015; Duijvestijn and Birchley, 1999): (1) the LH sited at the bottom of RPV is assumed to be fully submerged into water flooding; (2) The melting pool within the RPV is depressurized. However, the above assumptions weren't seriously challenged until the Fukushima accident on 2011 (An et al., 2016). The accident event showed that the structural behavior had not been appropriately assessed, and a certain pressure (up to 8 MPa) was found to exist at the inside (Mao et al., 2016a). Most notably, the malfunction of water supply system had occurred during the SA, resulting in insufficiency of cooling water on the external RPV wall (Government of Japan, 2011). Toward this end, the present paper tries to address the structural-related issue on whether RPV integrity can be secured within the prescribed period, if the RPV is subjected to various thermal-mechanical loads created during such a severe accident.
As for the structural-related issue under the IVR condition, the particular concern is to characterize the timing, mode, and size of a possible RPV failure with varying parameters such as water levels, internal pressures, since the structural safety is a requirement of paramount important in the operation of NPP (T. H. Kim et al., 2015). During the SA, the IVR mitigation should be robust and capable of maintaining the RPV in a manageable state and preventing the collapse of LH (Li et al., 2015). As mentioned previously, the depressurization of primary system was the basic assumption in the conventional IVR concept, so the traditional methodology takes effect only in a limit design basis accident (Mao et al., 2016b). As a matter of fact, the RPV failure can be affected by numerous factors, such as internal pressure and water cooling state. Due to the intrinsic limitation, the structural behaviors weren't fully understood for the RPV with various water levels under pressurized melt pool. Some of the failure mechanisms hadn't been recognized across the wall thickness using the traditional IVR concept (Zhu et al., 2017). As indicated in previous studies, at the low pressures, the creep failure mechanism dominates the failure process, whereas the plasticity becomes increasingly important at higher pressures (Duijvestijn et al., 2006). Some researchers pointed out that the higher internal pressure gave rise to the instant plastification, and inevitably aggravates creep deformation (Park et al., 2015). In most accident situations, the RPV safety should be ensured during the first 72 h, so it leaves enough time for the operator to take some emergence measures (Mao et al., 2016a). However, certain thermal-mechanical loading processes (or history) may accelerate or delay RPV failure time (Tsai et al., 2017; Tusheva et al., 2015). Furthermore, the failure mode as well as site can be significantly different for various loading situations. For instance, the unexpected malfunction of water supply system leads to various cooling water levels, resulting in the larger stored heat inventory due to the insufficiency of water cooling (Government of Japan, 2011). In fact, the continuing decay heat generation and the possibly high internal pressure are the acute and long term challenge to the RPV safety. As discussed previously, the external cooling state is the essential for ensuring the RPV integrity. Although the early vessel failure isn't allowed in most situations, the RPV will eventually fail unless the decay heat can be completely removed by the water cooling (Mao et al., 2016b). Accordingly, the RPV failure is determined as time- and temperature-dependent process. In disclosing the complexity of the structural behaviors, several experimental programs such as FOREVER, USNRC/SNL, CORVIS, and LIVE had been performed (Willschutz et al., 2001, 2006; Nicolas et al., 2003; Adroguer et al., 2003; Gaus-Liu et al., 2010; Buck et al., 2010), the results of which validated the predictability on the failure time, mode and site by using the finite element method (FEM). The already conducted experiment span a wide range of pressure (0.2–10 MPa) and temperature gradient (130–1500 ∘C) (Theofanous et al., 1997). Besides, the experimental data were also compared with the results by FEM in terms of field parameters, such as temperature, wall enlargement, wall thinning (Song et al., 2009). The results had revealed that the structural behavior was governed by the multilayer failure mechanism (Mao et al., 2016c), and the geometric discontinuity was most vulnerable to RPV failure (Mao et al., 2016d). Actually, the RPV integrity under SA was compromised by various failure mechanisms, such as melt-through, plasticity, thermal-plasticity, creep, and even necking. However, the influence of various water levels and internal pressures on RPV integrity is scarcely found in the previous studies. Therefore, a good understanding of structural behavior is of vital importance for ensuring the RPV safety in the above SA conditions.
In this paper, the main task is to numerically investigate the RPV structural behaviors with the effect of various water levels and internal pressures. Toward this end, the 2-D FE-models of the RPV were established on the ABAQUS platform. In order to illustrate the effect of various water levels on the structural behavior, three typical water levels were considered in FEA, including low, mid and high water levels. Due to the melting pool on the inside and external water cooling on the outside, the high temperature gradient is formed from 150 to 1327 ∘C across the wall thickness. Accordingly, the RPV failure is governed by several mechanisms, including creep, plasticity and thermal-plasticity. With the thermal-mechanical loadings, the structural behaviors of the RPVs are comparatively investigated in terms of temperature, deformation, stress, plastic strain, creep strain, and total damage. Due to the time- and temperature-dependent characteristics, both creep and plastic deformation are analyzed during the IVR condition, including the interaction between creep and plasticity. Through vigorous investigation, it is found that the failure site, mode and time are greatly affected by the water levels. Furthermore, the internal pressure plays an important role in determining the RPV failure.
2.1 Creep and plastic damage modeling
As is well known, the severe accident condition leads to the form of high temperature gradient across the RPV wall thickness. The inner surface of RPV is exposed to the pressurized melting pool, so the material temperature on the inside exceeds the 0.4 time of the melting point (1327 ∘C). Due to the high temperature on the inside, the creep failure mechanism occurs at the corresponding site. In describing the creep behavior of the RPV wall, the creep law (Mao et al., 2016d) with a number of free parameters is formulated as follows,
Wherein, the d1, d2, d3, d4 are material coefficients by fitting the creep law to test data obtained at constant load and temperature. As for the RPV steel, its creep process experiences primary, secondary and tertiary stages. Eq. (1) is a general form of strain hardening representation, and it has the capability in describing the above highly-nonlinear process. However, the requirement of the d1>0 and d3>0 must be satisfied. As indicated in Eq. (1), the material coefficients are rate- and temperature-related parameters. In order to have a proper parameter fitting, a newly-proposed subroutine with nonlinear weighting method is implemented in the ABAQUS. For plasticity, the stress–strain relationship is highly nonlinear, so the Ramberg–Osgood (R–O) equation is adopted for describing the material constitutive relationship,
Wherein, σ and ε are the true stress and true strain respectively, E is Young's modulus, σy is the yield strength, α and n are the material constants that can be fitted with the tensile data ranging from the yield point to the necking point. In the FE calculation, the option of multi-linear isotropic hardening is activated in ABAQUS for higher accuracy.
In fact, the plastic yielding and creep deformation occurs at the failure site simultaneously, so the “ductility failure criterion” is used for evaluating the damage. The material damage due to the significant plastic and creep strains is formulated by a damage measure D, which is the result of plastic damage increment plus creep damage increment. The increment ΔD is accumulated at the end of a load step or sub-step of the FEA, the expression of which is described as,
In Eq. (3), the and are creep and plastic rupture strain respectively, which can be obtained by the tensile test with constant thermal-mechanical loads for RPV material. It should be noted that the damage behavior is in dependence on the triaxiality factor Rv that is also incorporated in the “ductility failure criterion”,
Where, σH is the hydrostatic stress, σM is the von-Mises equivalent stress, v is the Poisson's ratio. The presence of is to reflect the effect of multiaxial stress state on damage evolution of RPV component. With the linear accumulation rule, the accumulated total damage D can be computed by the sum of each damage increment ΔD,
Actually, when the total damage D of an element is equal to 1, the element is deactivated by multiplying its stiffness matrix with a factor of 10−6, so the element is correspondingly set to be inactive using element death technique. If the ΔDi=0, the element has “no damage increment” at the specific sub-step.
2.2 Description of FE modeling
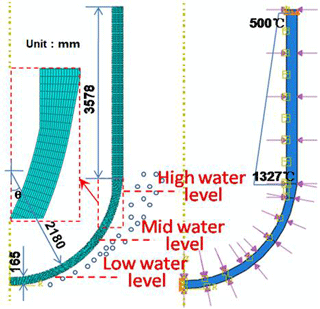
Due to the high nonlinearity characteristics in material properties, geometric configuration and loading, the analytical modeling is almost impossible for evaluating the structural behaviors. In overcoming this problem, the two-dimensional (2-D) FE-models are developed for the RPV with various water levels using ABAQUS platform, which is displayed in Fig. 2. In order to reduce the computational cost, only half part is considered in the FEM, due to its axisymmetry. Actually, the RPV structural behavior is very complex among the LH wall, so the wall thickness is intensively meshed. It can be seen in Fig. 2 that the grid density is aggravated at the transition portion of spherical segment to cylindrical segment. The mesh of LH wall is made of 20 nodes, and the element size is about 8 mm in width. After repeated convergence computation, the total element number is finalized to be 4200. Since the severe accident condition leads to the coupling of thermal-mechanical structural behavior, the thermal-coupled element type of CAX4T is employed in FEM, which is the 2-D structural 4-node iso-parametric element. The selected element type is suitable for computing time- and temperature-dependent deformation. It also has the capability in accounting for the creep and plasticity simultaneously. Due to the larger deformation, it provides more flexibility for considering the geometric nonlinearity, e.g. large plastic or creep deformation.
As for the boundary condition, the internal pressure is applied as a surface load on the inside of the RPV. Actually, the internal pressure load leads to an increasing primary stress with ongoing plastic and creep deformation. Two phenomena are directly related to the pressure load: (i) the enlargement of the bulk; (ii) the reduction of the wall thickness. As to thermal condition, the simulated tests showed the temperature on the inside was maintained at approximate melting point of 1327 ∘C, while the one on the outside was maintained at the level of nuclear boiling (∼150 ∘C). In order to account for the most dangerous thermal loading before the melt-through of the RPV wall, the critical heat flux (CHF) loading is considered herein. In addition to that, the various water levels are also considered in the FEM, due to the possibility of cooling system malfunction during the severe accident. As shown in Fig. 2, the low, mid and high water levels are adopted in the comparative analysis. At the RPV wall above the water level, the nature convection cooling is assumed in thermal boundary condition. In the empty chamber, the heat transfer processes are governed by the radiative transfer. For simplicity, the radiative heat flux is converted into thermal loading, so the equivalent temperature is obtained and applied on the cylindrical surface. Besides, the equivalent temperature is assumed to be linearly distributed along the cylindrical segment. It should be pointed out that the adopted RPV is drawn from the real component of AP600-type power plant. The basic geometric sizes are plotted in Fig. 2. For instance, the radius of the spherical portion is 2180 mm, and the wall thickness is 165 mm. The height of cylindrical segment is big enough to allow the enlargement of the LH, so the end effect is insignificant for the LH. Furthermore, the wall thickness of spherical segment to cylindrical segment is gradually increasing from 165 to 180 mm. As to constraint boundary conditions, Fig. 2 shows the zero horizontal displacement (Ux=0) at the symmetry axis, and the zero vertical displacement (Uy=0) at the top end of cylindrical segment.
3.1 The general analysis on field parameters
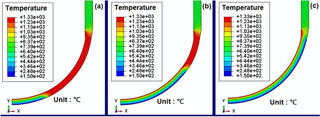
As illustrated in Fig. 2, the cooling water level varies with various water supplies during severe accident situations. Actually, sufficient flooding for external reactor vessel cooling (ERVC) isn't guaranteed as desired in most cases. As required in NRC regulation and design standard, the IVR-ERVC strategy should come into action successfully, although the insufficient water cooling may occur in the severe accident due to the malfunction of the supply system. However, the reality may not be in the assumed way. As indicated in Fukushima accident on 2011, the RPV structural integrity was greatly threatened by the insufficient water cooling, and the RPV failure took place before prescribed safety time of 72 h. Accordingly, it is important to know the temperature distribution for the RPVs with various cooling water levels. During the period of severe accident, the so called “IVR-ERVC” strategy is assumed to be able to arrest the degraded melting core within the lower head (LH), so the melting pool is formed on the inside. Consequently, it can be seen in Fig. 3 that the temperature on the inner surface is at approximate melting point (1327 ∘C) of RPV material. As for the outer surface of the LH, the temperature distribution varies with various cooling water levels, as shown in Fig. 3. It can be learnt that the water cooling significantly lowers the temperature on the outside, while the temperature becomes homogeneous on the RPV wall without water cooling. The observation of Fig. 3 reveals that the high temperature gradient is formed from 1327 ∘C on the inside to 150 ∘C on the outside across the wall thickness for the portion below the cooling water level. Clearly, Fig. 3 shows that the high temperature zone is significantly decreasing with increasing the water level. Figure 3 also indicates that the high temperature gradient exists at the site aside around the water level. Since the cylindrical segment is above the melting pool, the temperature of the corresponding wall thickness is mainly affected by the thermal radiation. From Fig. 3, it can be seen that the temperature of cylindrical segment is much lower than the one of the LH.
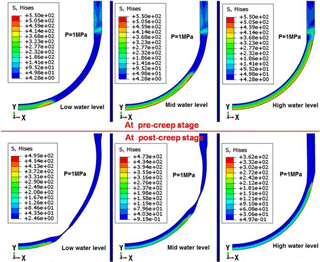
In accordance with the aforementioned basic scenarios, Fig. 4 plots the Mises stress contours for RPVs with various water levels at pre- and post-creep stages. The comparison of Fig. 4 discloses that the Mises stress is relaxed very significantly after a certain period of creep, especially for the inner surface of the RPV. Clearly, it can be seen in Fig. 4 that the Mises stress at high temperature zone is much lower than that at the water-cooled zone. There exists a highly-concentrated zone for the Mises stress at the site aside around the water level. The maximum value of Mises stress is found to be around 550 MPa at pre-creep stage. After a certain period of creep time, the lower head (LH) suffers great deformation, as indicated in Fig. 4. For RPV with low to moderate water level, the necking phenomenon is found at the transition region above the water level, while the RPV with high water level still has some load-carrying capability in preventing necking. Close observation of Fig. 4 reveals that the RPV with low water level is most vulnerable to structural failure after a certain amount of creep hours. After a period of creep, the Mises stress field is redistributed into a new one for the three RPVs. Although the stress relaxation somehow occurs throughout the whole region, the phenomenon of stress concentration still exists at the site in the proximity of water level at post-creep stage. As indicated in Fig. 4, for the RPV with low to moderate water level, the RPV structure must undergo severe plastic and creep deformation at the weakest link of the wall thickness, since the RPV wall necking is ductile failure mode. It can also be inferred in Fig. 4 that the maintenance of structural integrity highly depends on the cooling water level under severe accident scenario.
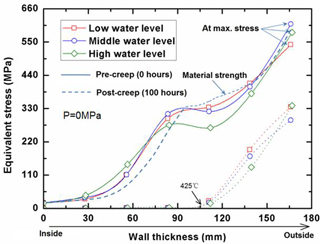
As is well known, the yield limit of RPV material is decreasing with increasing the temperature, which is depicted as the symbol of dash line in Fig. 5. Taking the yield limit as a failure criterion, it can be observed in Fig. 5 that the wall thickness of inner surface to mid layer is almost performed in the state of plasticity, because the equivalent stress computed by FEM exceeds the yield limit at the corresponding site. More interestingly, there exists a core of elastic layer within the wall thickness, as shown in Fig. 5. The elastic core is squeezed into a very small region with lowering the cooling water level, implying that the load-carrying capability is correspondingly decreasing. As a matter of fact, the existence of elastic core is essential for ensuring the RPV safety under SA condition, since the elastic core has some load-carrying capability in preventing immediate collapse locally. For the outer surface layer, the equivalent stress is approaching the yield limit as it increases with decreasing the temperature. Taking the creep effect into account, it can be observed in Fig. 5 that the stress is relaxed very significantly within the wall thickness of mm, which is reduced to near stress-free level for the wall thickness of T>425 ∘C. Moreover, the stress on the outer surface layer is found to be relaxed by approximate 40 %. General observation of Fig. 5 displays that the stresses of RPV with various water levels are arranged as low water level > mid water level > high water level.
3.2 The effect of creep on plastic strain of RPVs
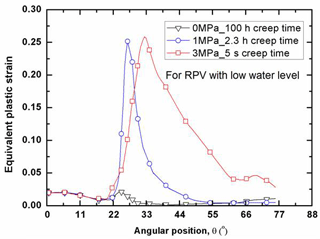
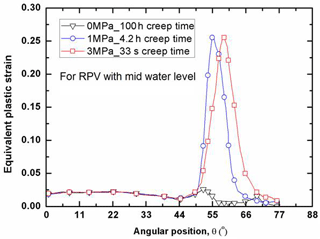
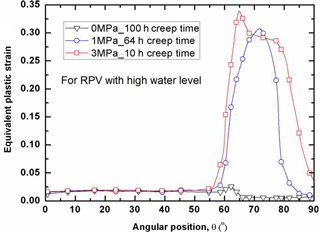
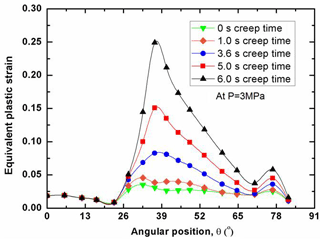
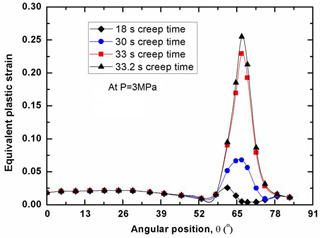
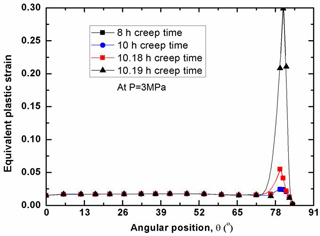
As for the structural integrity assessment, it is interesting to examine the distribution of plastic strain at the failure time. With the effect of creep on the plastic strain, the plastic strain distribution varies with the creep time, since the creep is a time-dependent process. Due to the existence of the primary pressure on the inside of the RPV, the failure time also varies with the water levels for the RPVs. Figure 6 shows that the distribution of equivalent plastic strain along the lower head (LH) with low water level. In order to make a judgment on the RPV safety, the plastic limit of εp=0.25 is taken as a basis for comparison. It can be seen in Fig. 6 that the internal pressure plays an important role in determining whether the RPV integrity is maintained or not after a certain period of creep time. At the low to moderate pressure levels (P<1 MPa), the most significant plastic strain is concentrated at the site near the water level. With the increase of internal pressure, the equivalent plastic strain spreads out over a wide area above the water level of the LH. As indicated in Fig. 6, the plastic strain is insignificantly distributed among the LH without the internal pressure effect after 100 creep hours, whereas the maximum plastic strain abruptly increases up to the plastic limit of εp=0.25 after 2.3 creep hours with the internal pressure loading of 1 MPa. Most notably, the comparison in Fig. 6 demonstrates that the LH may fail locally at the site in proximity of low water level as soon as 5 s under the internal pressure loading of 3 MPa, due to its significant plastic strain computed by FEM exceeding the plastic limit of the RPV material. Besides, in order to illustrate the instant structural behavior under the various internal pressure loads, Figs. 7 and 8 plot the distributions of plastic strain for the RPV with mid and high water level respectively. Through the comparison, it can be found that the most significant plastic strain always occurs at the location near water level. In other words, the corresponding site is most vulnerable to failure, due to the unacceptable plastic yielding. Clearly, both Figs. 7 and 8 show that the maximum plastic strain exceeds the plastic limit with the effect of internal pressure. It can be observed that the highly-plasticized zone is enlarged with the increase of internal pressure. General observation of Figs. 6, 7 and 8 reveals that the high plastic strain spreads over the high temperature zone above the water level, especially for the condition of high internal pressure loading. Besides, it should be noted in Figs. 6, 7 and 8 that the failure time of the LH is different from each other. Due to the existence of certain internal pressure, the failure time is remarkably reduced accordingly by comparing with the one without internal pressure. It can be learnt that the RPV fails at the time of 2.3, 4.2, 64 h for the respective situation of low, mid and high water level under internal pressure loading of 1 MPa. If the internal pressure is further increased up to 3 MPa, the failure time of RPV is lowered down to 5, 33 s, 10 h for the respective water level under the loading of 3 MPa. From this perspective, it is safe to say the RPV with high water level has most advantage in preventing the immediate structural failure, the reason for that can be attributed to the well maintenance of the material strength in the outer layer of wall thickness. As for the RPV wall thickness below the water level, the plastic strain is insignificantly distributed, most of which is less than εp=0.025. Under the present severe accident conditions, it can be seen that the cooling water level determines the failure site, and the failure time is greatly affected by the internal pressure. Also, it can be concluded from Figs. 6, 7 and 8 that the global failure isn't a feasible mode for the RPV under primary pressure loading.
As mentioned before, the time-dependent creep plays an important role in affecting the RPV structural failure process. Also, the plastic strain profile varies for the RPVs with various water levels, as shown in Figs. 9, 10 and 11. As a matter of fact, the higher internal pressure gives rise to plastic strain rather than creep strain immediately after the load is applied on the RPV. With the increase of the creep time, the creep strain accumulated on heat-focused zone may be larger than the instant plastic strain. As for the RPV with low water level, Fig. 9 shows that the plastic strain significantly increases with the creep time, especially at the site aside around the water level. After creep time of 6 s, it can be seen in Fig. 9 that the maximum creep strain reaches the value of εp=0.25 with the loading of 3 MPa. Figure 9 also reveals that the creep accelerates the plastic strain evolution, and the plastic strain become increasingly significant among the region in the proximity of water level. At the wall thickness below the water level, there is no significant change for the plastic strain distribution, and the corresponding plastic strain is maintained at a relatively low level throughout the whole creep process. The comparison of Figs. 9, 10 and 11 discloses that the highly-plasticized zone is squeezed into a smaller size with increasing the water level. Accordingly, the plasticized zone is the smallest one for the RPV with high water level, as shown in Fig. 11. Most notably, it can be found in Figures that the evolution of plastic strain become very sensitive to the creep, when the failure time is exceeded. In other words, it can be inferred that the interaction between plastic and creep strain becomes much severer after the failure time. Finally, the RPV failure (or collapse) is triggered by the creep evolution, and is contributed by the sum of plastic and creep strain. Again, it can be concluded from the above analysis that the RPV must collapse or fail locally at the site near the water level. The comparison of Figs. 9, 10 and 11 discloses that the RPV with high water level has the most ability in preventing RPV failure.
3.3 The effect of water levels on creep strain of RPVs
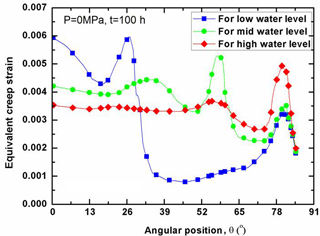
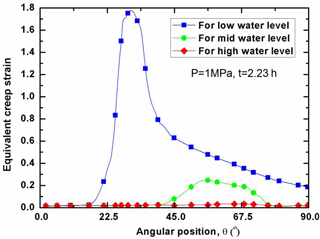
As indicated above, the creep strain makes a great contribution to the RPV failure. In illustrating it, Fig. 12 plots the distribution of equivalent creep strain (simply called as “CEEQ”) along the LHs without internal pressure effect for the condition of various water levels. It can be seen in Fig. 12 that the peak value of CEEQ occurs at the site aside around the water level, correspondingly at the low, mid and high angular position. The comparison of Fig. 12 shows that the maximum creep strain is arranged as the one of low water level > mid water level > high water level. Before the peak value of creep strain, there exists a significant fluctuation of the creep strain, due to the deformation incompatibility. At the transition portion of spherical to cylindrical segment, a small peak value of creep strain is found correspondingly for the RPV with low and mid water level. Throughout the whole lower head, it can be found in Fig. 12 that the maximum creep strain reaches the value of 0.6 % without consideration of the internal pressure effect. For the RPV with low water level, the creep strain at the high temperature segment is maintained at a relatively low level except at the transition location of hot and soft to cool and strong wall thickness.
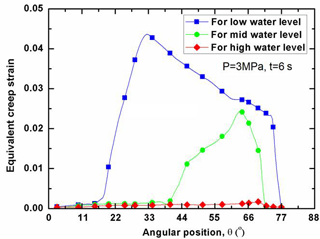
With the increase of internal pressure, the creep strain is significantly increased at the failure time for the condition of respective water level. Figures 13 and 14 plot the distributions of CEEQ along the LH under the internal pressure of 1 and 3 MPa respectively. Figure 13 shows that RPV with low water level suffers the severest CEEQ at the transition site of cool to hot wall segment. For the RPV with mid water level, the high CEEQ is distributed widely among the transition location, whereas the CEEQ is insignificantly distributed throughout the LH for the RPV with high water level. Compared with Fig. 13, it can be seen in Fig. 14 that the high CEEQ zone becomes much wider with increasing the internal pressure. Again, both Figs. 13 and 14 display that the maximum CEEQ occurs at the site aside around the water level. Still, the RPV with high water level has the lowest CEEQ at a specific time. At the internal pressure of 3 MPa, the CEEQ exceeds the value of 2.5 % for most of the LH wall thickness, indicating that the significant creep damage for the corresponding RPVs with low to mid water level, as shown in Fig. 14. As compared to the one in Fig. 12, it can be observed in Figs. 13 and 14 that only one peak value of CEEQ take place across the whole LH for the condition of 3 MPa. Furthermore, the peak value does not exist at the transition portion of spherical segment to cylindrical segment.
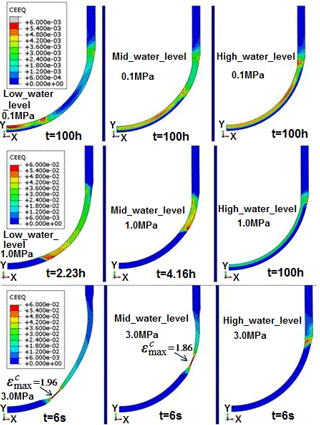
In order to visualize the distribution of creep strain across the whole LH, Fig. 15 plots the equivalent creep strain (simply called “CEEQ”) contours for RPV with various cooling water levels and internal pressures. The overall observation of Fig. 15 discloses that the maximum creep strain occurs at the location of wall thickness in proximity of water level. It should be noted in Fig. 15 that the LH creep deformation under the low to mid pressure is not accompanied by the essential vessel wall thinning, and its failure is caused by the accumulated creep strain during the IVR process. However, under the high internal pressure (3 MPa), the accumulated CEEQ results in the significant deformation, even necking phenomenon for the RPV with low to mid water level, as shown in Fig. 15c. The severest CEEQ reaches the value of approximate 1.90 at the failure site after 6 s creep time. From this perspective, the existence of internal pressure is very detrimental to the RPV safety during the severe accident. Combined with the above analysis on the plasticity, it can be concluded that the plastic and creep strains are interacted with each other. The results indicate that the location of failure zone caused by plastic strain coincide with the one by creep strain. Again, it can be found in Fig. 15 that the RPV with low water level is most vulnerable to structural failure under the condition of severe accident, since the concentration of CEEQ at the failure site is the severest among the three cases. Close observation of Fig. 15 reveals that the significant CEEQ takes place on the inner surface of the LH at low pressure, whereas the higher CEEQ occurs on the outer surface at mid pressure, and finally the higher CEEQ zone is interlinked across the wall thickness of the failure site at high pressure. This phenomenon can be attributed to the variance of deformation incompatibility with the effect of various internal pressures. The variance of higher CEEQ distribution will inevitably lead to the corresponding failure initiation. At a constant low pressure, the failure initiates at the inner surface, while with further increase of internal pressure, the outer surface tends to undergo more creep deformation. Actually, it can be inferred in Fig. 15 that the creep effects dominate the LH failure process at low to moderate pressures, and instant plasticity becomes increasingly important at higher pressures.
3.4 The evaluation on RPV structural failure behaviors
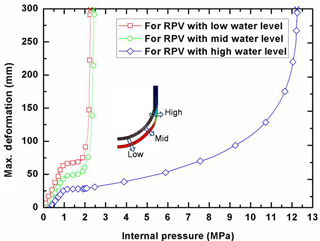
As indicated above, the final RPV failure (or collapse) is caused by the combination of plastic and creep deformation. In order to illustrate the failure process, Fig. 16 plots the relationship of the maximum deformation vs. internal pressure for the RPV with various water levels. It can be seen in Fig. 16 that the deformation at post-creep stage is shown as a nonlinear function of the internal pressure. Clearly, for the condition of low to moderate internal pressure, the bulge of LH is abruptly increasing at the internal pressure of approximate 2.25 MPa, whereas the LH with high water level significantly stretches outward at the site near the water level for the condition of more than 10 MPa. Through careful observation, it can be found that the maximum deformation occurs at the failure site in proximity of corresponding water level. Further observation of Fig. 16 shows that the max. deformation is increasing very fast at the internal pressure of less than 1 MPa, and then it stably increases up to a certain value at the internal pressure from 1 to 2.25 MPa. Furthermore, Fig. 16 demonstrates that the max. deformation is arranged as the one with high water level > the one with mid water level > the one with low water level, throughout the spectrum of internal pressure. In fact, the max. deformation of the LH is contributed by the thermal expansion, plastic yielding and creep accumulation. As well known, the thermal expansion is a constant value with the fixed temperature distribution, so the relationship of max. deformation vs. internal pressure is dominated by the plastic and creep deformation at the corresponding site.
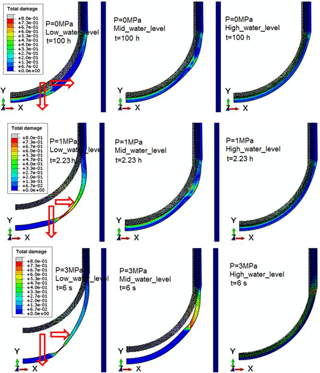
As mentioned before, the final RPV failure is caused by the plastic and creep damage. In order to visualize the total damage distribution, Fig. 17 plots the contour of total damage for the RPVs with various water levels under various internal pressures. As can be seen from Fig. 17, the bulge of the LH is observed for all the mentioned cases. It stretches outward along both horizontal and vertical direction, and the displacement along the vertical direction is much larger than the one along the horizontal direction. With the increase of internal pressure, the LH stretches out more and more significantly, especially for the RPV with low water level. For the condition of low to moderate pressure, the maximum displacement of the vessel wall has reached up to 50 mm at the failure time. Clearly, the sagging of the deformed LH could be several times larger than the initial undeformed LH, and the deformed LH shape is appeared as an “egg shell” after a period of creep time. It is clear to see from Fig. 17 that the sagging is associated with severe necking phenomenon at the failure site, especially for the RPV with low water level. During the creep period, the wall thinning is observed for all the mentioned cases. For instance, the most significant reduction of wall thickness is reached up to 25 % at creep time of 2.23 h for the RPV with low water level under internal pressure of 1 MPa. For the case with low pressure and high water level, the damage is highly concentrated on each side of wall thickness near water level. It can be seen in Fig. 17 that the damage in the middle layer of the wall thickness is much lower than the one on surface layer at the initial creep stage, due to the existence of elastic core. However, with the aggravation of creep damage, the development of plastic damage must be accelerated, so the total damage evolves much faster with increasing creep time. It can be inferred that the creep and plastic damages are interacted with each other. Accordingly, time- and temperature-dependent analyses are necessary for assessing the RPV safety under severe accident condition. Consequently, the nonlinearities, large displacement, large strain and follower damage, must be taken into account in the finite element analysis (FEA). Furthermore, one can note that the calculated sagging and cumulated damage is greatly affected by the internal pressure and external water level. With the effect of internal pressure, the RPV failure time significantly decreases. As for the RPV with low water level, the failure time is >100 h, 2.23 h, 6 s corresponding to condition of 0.1, 1, 3 MPa, since the highest damage exceeds 1. Moreover, the observation of Fig. 17 reveals that the localized failure is the feasible failure mode, and the RPV instability takes place at the transition portion of cool to hot wall thickness. Due to the large elongation aside around the failure site, the failure process presents ductile behavior, so the final failure is caused by the combination of ductile tension and shear. Accordingly, the instant global collapse is impossible immediately after the thermal-mechanical loading is applied on the LH.
In the current paper, the RPV with various water levels is chosen for study, due to the possibility of water cooling system malfunction under severe accident of core meltdown. As indicated in some severe accidents, a certain pressure (up to 8.0 MPa) may exist inside the RPV, so the scenario of pressurized core meltdown is considered in the FEM. In order to illustrate the structural behavior and its failure, the thermal-elastic-visco-plastic FE models are developed in the platform of ABAQUS with consideration of highly nonlinear characteristics. Due to the presence of the melting pool (∼1327 ∘C) at the inside and external cooling water (∼150 ∘C), the most dangerous thermal loading is considered and applied on RPV wall as the type of critical heat flux (CHF) loading before the material melting of the wall thickness. Actually, the severe accident condition leads to the formation of high temperature gradient, so the RPV structural behavior spans a wide range of failure mechanisms, such as creep deformation and plastic yielding. Through vigorous FE investigation, the main results can be summarized as follows:
-
Due to the existence of various water levels, the temperature fields are quite different from each other, resulting in significant variation of structural failure site, time and mode for the RPVs. It is found that the increase of cooling water level improves the RPV structural safety, that is to say, the corresponding IVR strategy is enhanced.
-
The failure site takes place at the location in the proximity of cooling water level, since the total damage is highly concentrated at the site. At the low pressure (≤1 MPa), the RPV tends to globally stretch outwards, whereas the localized ductile failure is the failure mode at higher pressure (≥3 MPa), especially for the RPV with low to moderate water level.
-
Due to the existence of elastic core in the midpoint of wall thickness for some cases, the damage distributed around aside each surface of RPV wall may well exceed the one at midpoint. Further analysis shows that the plastic damage at failure time accounts for approximate 80 % of total damage for the cases with low water level, while the evolution of total damage is significantly accelerated by creep.
-
The stress on the inner surface is unanimously relaxed to a near-zero level at failure time, while the stress (strain) field is varying during the IVR period. Due to the incompatible deformation, the RPV wall at around the water level suffers severe stress triaxiality, which exacerbates the RPV failure process. Through the analysis, it is found that the existence of internal pressure at any level is a huge threat to RPV integrity, so the pressure release is necessary to IVR strategy.
-
The RPV enlargement is observed throughout the whole failure process, the wall thickness is simultaneously thinning all over the time, especially for the failure site. With the increase of internal pressure, the vertical bulge of RPV is much larger than the horizontal bulge. Furthermore, the most significant bulge is found at the failure site for the RPV with low water level.
The underlying data are available upon request. The data presented herein can be cited in scientific work, however, any real project in using the present data must be approved by the authors who hold the right.
| d1–d4 | material parameters in creep equation |
| D,ΔD | the damage, damage increment |
| Rv | the triaxiality factor |
| T | temperature |
| v | Poisson ratio |
| creep strain rate | |
| ε;εp | the elastic plus plastic strain; the plastic strain |
| creep fracture strain | |
| plastic fracture strain | |
| α,n | material constants for R–O equation |
| θ | polar coordinate angle along lower header |
| σH | hydrostatic stress |
| σM | von-Mises stress |
| σus | ultimate strength |
| σy | yield strength |
The authors declare that they have no conflict of interest.
This work supported by National Natural Science Foundation of China (Grant
No. 51505425; 51575489), Zhejiang Provincial Natural Science Foundation of
China under Grant No. LQ15E050007; LY16E050012.
Edited by: Anders Eriksson
Reviewed by: Chang Yoon-Suk and three anonymous referees
Adroguer, B., Chatelard, P., and Van Dorsselaere, J. P.: Core loss during a severe accident (COLOSS), Nucl. Eng. Des., 221, 55–76, 2003.
An, S. M., Song, J. H., Kim, J. Y., Kim, H. Y., and Masanori, N.: Experimental investigation on molten pool representing corium composition at Fukushima Daiichi nuclear power plant, J. Nucl. Mater., 478, 164–171, 2016.
Buck, M., Burger, M., Godin-Jacqmin, L., Tran, C. T., and Chudanov, V.: The LIVE program – results of test L1 and joint analyses on transient molten pool thermal hydraulics, Prog. Nucl. Energ., 52, 46–60, 2010.
Duijvestijn, G. and Birchley, J.: Core melt down and vessel failure: a coupled problem, Nucl. Eng. Des., 191, 17–30, 1999.
Gaus-Liu, X., Miassoedov, A., Cron, T., and Wenz, T.: In-vessel melt pool coolability test-Description and results of LIVE experiments, Nucl. Eng. Des., 240, 3898–3903, 2010.
Government of Japan: Nuclear Emergency Response Headquarters, Report of the Japanese Government to the IAEA, Ministerial Conference on Nuclear Safety-The Accident at TEPCO's Fukushima Nuclear Power Stations, Vienna, Austria, 2011.
Jung, J., An, S. M., Ha, K. S., and Kim, H. Y.: Evaluation of heat-flux distribution at the inner and outer reactor vessel walls under the in-vessel retention through external reactor vessel cooling condition, Nucl. Eng. Technol., 47, 66–73, 2015.
Kim, S.-H., Chang, Y.-S., Song, S., and Cho, Y.-J.: Structural assessment of fully flooded reactor cavity and penetration piping under steam explosion conditions, Int. J. Pres. Ves. Pip., 131, 36–44, 2015.
Kim, T. H., Kim, S. H., and Chang, Y. S.: Structural assessment of reactor pressure vessel under multi-layered corium formation conditions, Nucl. Eng. Technol., 47, 351–361, 2015.
Li, Y. B., Tong, L. L., Cao, X. W., and Guo, D. Q.: In-vessel retention coolability evaluation for Chinese improved, 1000 MW PWR, Ann. Nucl. Energy, 76, 343–349, 2015.
Mao, J. F., Zhu, J. W., Bao, S. Y., Luo, L. J., and Gao, Z. L.: Creep deformation and damage behavior of reactor pressure vessel under core meltdown scenario, Int. J. Pres. Ves. Pip., 139, 107–116, 2016a.
Mao, J. F., Zhu, J. W., Bao, S. Y., Luo, L. J., and Gao, Z. L.: Investigation on structural behaviors of RPV with the effects of critical heat flux and internal pressure, J. Press. Vess.-T. ASME, 139, 021206, https://doi.org/10.1115/1.4034582, 2016b.
Mao, J. F., Li, X. Q., Bao, S. Y., Luo, L. J., and Gao, Z. L.: Investigation on multilayer failure mechanism of RPV with a high temperature gradient from core meltdown scenario, Nucl. Eng. Des., 310, 39–47, 2016c.
Mao, J. F., Zhu, J. W., Bao, S. Y., Luo, L. J., and Gao, Z. L.: Study on structural failure of RPV with geometric discontinuity under severe accident, Nucl. Eng. Des., 307, 354–363, 2016d.
Nicolas, L., Durin, M., Koundy, V., and Mathet, E.: Results of benchmark calculations based on OLHF-1 test, Nucl. Eng. Des., 223, 263–77, 2003.
Park, R.-J., Kang, K.-H., Hong, S.-W., and Kim, H.-Y.: Detailed evaluation of melt pool configuration in the lower plenum of the APR1400 reactor vessel during severe accidents, Ann. Nucl. Energy, 75, 476–482, 2015.
Schulz, T. L.: Westinghouse AP1000 advanced passive plant, Nucl. Eng. Des., 236, 1547–1557, 2006.
Song, H.-W., Nam, S.-H., Shim, B., and Kim, S.-H.: Path-dependent nonlinear analysis of a concrete reactor containment vessel subjected to internal pressure using a volume control technique, Eng. Struct., 31, 990–998, 2009.
Theofanous, T. G., Liu, C., Additon, S., Angelini, S., KymaHiinen, O., and Salmassi, T.: In-vessel coolability and retention of a core melt, Nucl. Eng. Des., 169, 1–48, 1997.
Tsai, F. J., Lee, M., and Liu, H. C.: Simulation of the in-vessel retention device heat-removal capability of AP-1000 during a core meltdown accident, Ann. Nucl. Energy, 99, 455–463, 2017.
Tusheva, P., Altstadt, E., Willschütz, H.-G., Fridman, E., and Weiß, F.-P.: Investigations on in-vessel melt retention by external cooling for a generic VVER-1000 reactor, Ann. Nucl. Energy, 75, 249–260, 2015.
Willschutz, H. G., Altstadt, E., Sehgal, B. R., and Weiss, F. P.: Coupled thermal structural analysis of LWR vessel creep failure experiments, Nucl. Eng. Des., 208, 265–282, 2001.
Willschutz, H.-G., Altstadt, E., Sehgal, B. R., and Weiss, F.-P.: Recursively coupled thermal and mechanical FEM-analysis of lower plenum creep failure experiments, Ann. Nucl. Energy, 33, 126–148, 2006.
Yue, J., Wei, X., Liu, X. J., and Cheng, X.: In- and ex-vessel coupled analysis of IVR-ERVC phenomenon for large scale PWR, Ann. Nucl. Energy, 80, 322–337, 2015.
Zhu, J. W., Mao, J. F., Bao, S. Y., Luo, L. J., and Gao, Z. L.: Comparative study on reactor pressure vessel failure behaviors with various geometric discontinuities under severe accident, J. Press. Vess.-T. ASME, 139, 021214, https://doi.org/10.1115/1.4035697, 2017.