the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Boundary-layer separation in circular diffuser flows in the presence of an external non-uniform magnetic field
Seyed Morteza Moghimi
Mehran Khaki Jamei
Davood Domiri Ganji
The focus of the present work is on the investigation of the separation point and its relative location in a circular diffuser carrying incompressible laminar flow in the presence of a non-uniform external magnetic field. Two different approaches are deployed in the present analysis. In the first approach, a similarity transform is applied to reduce the momentum equation to the nonlinear ordinary differential equation (ODE). The ODE is solved by a dual integral–numerical method and the separation position is directly determined. In this combined numerical–integral methodology, the integration is applied followed by a numerical method. In the second approach, the equation is solved by the least square method (LSM), and the separation position is indirectly specified. In this study it is shown that the magnetic field intensity can be manipulated to postpone the separation such that it could be eliminated totally. Comparing the results yields a good agreement. It has been concluded that by increasing the magnetic field intensity, as the Lorentz force increases, increased shear stress on the wall and delay in the occurrence of the separation position are observed.
Magnetohydrodynamics (MHD) is a physical–mathematical framework concerned with the dynamics of magnetic fields in electrically conducting fluids. It focuses on the interaction between the hydrodynamic boundary layer and the electromagnetic field. Today, the study of MHD flow is not only of increasing interest in studying fluid mechanics, but also for studies in many disciplines formulated as branches of physics including, but not limited to, mathematical or condensed matter physics, astrophysics, geophysics, and biophysics. According to the literature, in a wide range of research spectra, MHD and fluid dynamics are indispensable (Bhatti et al., 2018; Ghadikolaei et al., 2017; Hosseinzadeh et al., 2017; Jhorar et al., 2018; Regev et al., 2016). MHD has increasing applications in the fields of the aerospace engineering, environment engineering and sciences, chemical engineering, mechanical and biomechanical engineering, etc. One of its applications in material processing could be the control of molten metal flow by the magnetic field in the casting industry.
The governing equations of MHD radial flow were originally carried out by Jeffery (1915) and Hamel (1916). Steady-state incompressible flow through a parallel plate channel with stretching walls under an externally applied magnetic field has been studied by Abbasi et al. (2014). Taheri et al. (2017) presented analytical solutions to laminar flow of MHD Newtonian and non-Newtonian power-law fluids in the entrance regions of channels. They observed that an augmentation of the magnetic interaction parameter leads to a greater pressure drop in comparison with a typical hydrodynamic flow without the presence of a magnetic field. Khaki et al. (2014) studied a boundary-layer analysis of an incompressible viscous steady flow and forced convection over a horizontal flat plate.
An efficient computational technique was considered to be a modified decomposition method that was proposed and successfully applied for solving the nonlinear problem of the two-dimensional flow of an incompressible viscous fluid between nonparallel planes (Kezzr et al., 2015). There have been numerous studies focusing on Jeffery and Hamel's problem without considering the effect of magnetic fields, such as Bougoffa et al. (2016), Khan et al. (2016b), and Stow et al. (2001). To the knowledge of the authors, Axford (1961) was the first to study MHD flow in Jeffrey–Hamel problems. The study represented the exact solutions of the MHD equations for the radial flow of a viscous incompressible fluid between non-parallel walls. In that study, the reduction of the displacement thickness of the boundary layer due to magnetic field presence was observed. Sadeghy et al. (2007) studied a theoretical investigation of the applicability of magnetic fields for controlling hydrodynamic separation in Jeffrey–Hamel flows of viscoelastic fluids. Makinde (2008) investigated the effect of an arbitrary magnetic Reynolds number on a steady flow of an incompressible conducting viscous liquid in convergent–divergent channels under the influence of an externally applied homogeneous magnetic field. Ellahi et al. (2016) studied a Jeffrey fluid peristaltic flow in a non-uniform rectangular duct under the effects of Hall and ion slip. They showed that shear thinning reduces the wall shear stress. On the other hand, there has been a set of nearly-new tracks' semi-analytical and numerical solutions addressing the solution of the problem: the Adomian decomposition method (Ganji et al., 2011), the homotopy analysis method (Moghimi et al., 2011a) and the homotopy perturbation method (Moghimi et al., 2011b). Analytical exact solutions in the implicit form for further physical interpretation were presented by Abbasbandy and Shivanian (2012). As an efficient semi-analytical approach alternative to both numerical and exact (analytical) solutions, the variational iteration method was successfully applied by Mirgolbabae et al. (2009). Developing numerical techniques for a nonlinear MHD Jeffery–Hamel blood flow problem to analyze the behavior of blood flow and its contribution to high blood pressure through artificial neural networks trained with the Active Set and Interior Point Algorithm was used by Ahmad et al. (2014). However, analytical and numerical solutions for (MHD) Jeffery–Hamel nano-fluid flow have been frequently in articles (Alam et al., 2016; Ananthaswamy and Yogeswari, 2016). Khan et al. (2016a) have studied deals with the numerical investigation of Jeffery–Hamel flow and heat transfer in Eyring–Powell fluid in the presence of an outer magnetic field by using the Haar wavelet method.
According to the above survey, although the numerous investigations focused on MHD flows for different applications, the displacement of the separation point for MHD flows in circular diffusers by changing the magnetic field intensity has not been studied yet. The present work aims to fill this gap by deployment of two different approaches and eventually investigation of the accuracy of the solutions. The separation position is determined directly using the semi-analytical method and so indirectly by the least square method (LSM), and the effect of the magnetic field intensity on the displacement of the separation point is discussed in detail.
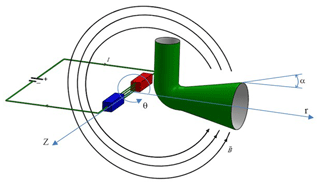
Consider a steady, laminar incompressible flow in a two-dimensional circular diffuser with a 2α expansion angle, under the influence of a non-uniform external magnetic field, as shown in Fig. 1.
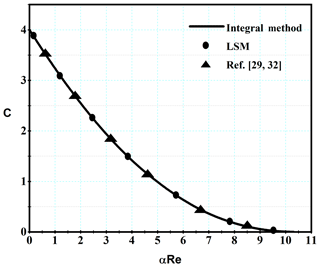
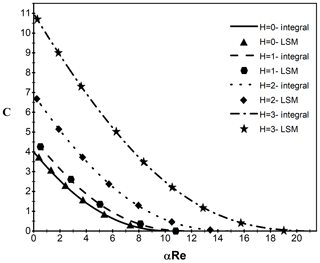
Figure 2The C–αRe curve comparison between the present work and references (Schlichting and Gersten, 2000; Withe, 2006).
The r and θ axes are defined as the usual polar coordinate, whereas the r axis corresponds to the direction of the flow and lies on the center line. The flow velocity distribution is considered to be . The general governing equations for the defined problem are defined as (Davidson, 2001; Schlichting and Gersten, 2000)
Eqs. (1) to (3) are continuity, momentum and Ohm's law, respectively. The V, J, E, P, σ and B are the velocity vector, the electric current density, the electric field, the pressure, the electrical conductivity and the total magnetic field, respectively. The total magnetic field is , where B0 is the external magnetic field and b is the magnetic field induced. In the problem, the magnetic Reynolds number is assumed to be small enough, so that the induced magnetic field can be neglected (Roidt and Cess, 1962). The boundary conditions are defined as follows:
Define η, U(η), the Reynolds number (Re) (28) and the Hartmann number (Ha) as:
By substituting Eq. (5) into Eq. (2) and after some simplification, we have
Then the boundary conditions are transformed to
The solution of the problem is obtained by means of the two different approaches. In the first method, a dual integral–numerical method (DINM) is employed, and then the separation point was obtained directly. In the second approach, the LSM is used, and the separation point is obtained, indirectly. Furthermore, the fourth-order Runge–Kutta numerical method is used for the validation.
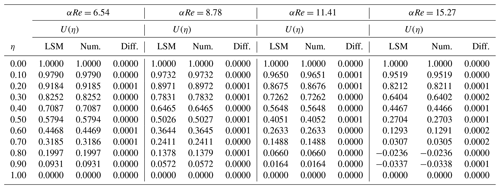
Table 1The dimensionless velocity distribution comparison for the LSM and the numerical method at Ha=1, , and (αRe).
3.1 Integral–numerical method
At the separation point, the shear stress vanishes, so the separation occurs if
Thus, according to Eq. (6), we can write
In the following, U′(η) is analyzed. Equation (6) is integrated with respect to η as
where “s” is constant. Multiplying Eq. (10) in 2U′ and integrating again give
Using boundary conditions Eqs. (7a) and (7c) and doing some algebraic manipulations, we will have
Applying Eq. (7b) in Eq. (12) gives
According to the above equation, if C equals zero, the shear stress at the wall becomes zero. By using Eqs. (7a) and (7b) we can write
Combining with Eq. (12), we will have
For small α and large Re, Eq. (15) simplifies as follows:
The trial and error technique is used for solving Eq. (16). It is divided into two parts as follows:
For a given value of the Hartmann number, the different values can be attributed to K. For each case, αRe is obtained from Eq. (17). By substituting Eq. (17) into Eq. (18), the value of C will be obtained. By considering that K equals zero, the shear stress becomes zero at the wall, according to Eqs. (13) and (18). Thus, at the separation point, Eq. (17) is simplified as
In order to solve Eq. (19), for different Ha, a numerical method is used by trial and error. For accuracy control a comparison between the results obtained from the present work and that by the references (Schlichting and Gersten, 2000; Withe, 2006), for Ha=0, is shown in Fig. 2. It can be observed that there is an excellent agreement among them.
3.2 Least square method
The dimensionless velocity distribution for the separation region, which is adjacent to the separation point (corresponds to (αRe)sep.), is obtained by the solution of Eq. (6) using the least square method (Moakher et al., 2016; Vahabzadeh et al., 2015). Owing to that the boundary conditions must satisfy the trial solution; the trial solution can be assumed as
For example, when Re=150, and Ha=1, by substituting Eq. (20) into Eq. (6) one equation with seven unknown coefficients is obtained. With some algebraic manipulation and by derivation with respect to each coefficient, seven equations with seven unknown coefficients are generated. The coefficients are calculated by solving the system of equations. Then by substituting the coefficients into the trial solution, the dimensionless velocity profile is determined as
Now, Eq. (21) is differentiated with respect to η; then,
The value of C is defined according to Eq. (13), and then we will have
In the same way, the value of C is calculated for the different values of αRe and Hartmann number. To verify, the results of the integral method and the LSM are plotted in Figs. 2 and 3.
Table 1 represents the results for the dimensionless velocity field, obtained from the two different approaches, which are employed in this study, i.e., the numerical method and the LSM. Comparing the results shows a reasonable agreement between them.
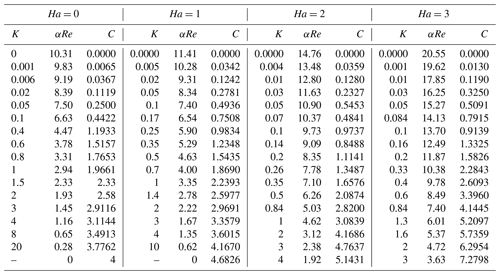
In Table 2, the results obtained from DINM are presented. The first row of the table shows the separation point information (corresponds to C=0), and it can be seen that as the Ha number increases, the value of αRe in which the separation occurs increases as well. It should be noted that α times Re is correlated with radial position and for the specified problem the separation occurs further downstream at distance from the inlet.
In the physical aspect, the Lorentz force is proportional to velocity, and it has a higher value in the center region. As a result, the velocity profile becomes flatter by imposing a higher magnetic intensity. Thus, for a certain velocity at the diffuser inlet, the momentum becomes higher near the wall by imposing the magnetic field and separation shifts downstream. Also, with an increasing magnetic field (Hartmann number), the Lorentz force increases, so that the separation is delayed and the αResep. value increases as shown in Fig. 3.
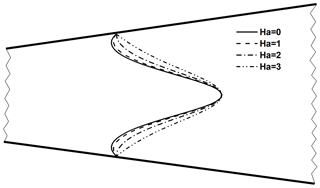
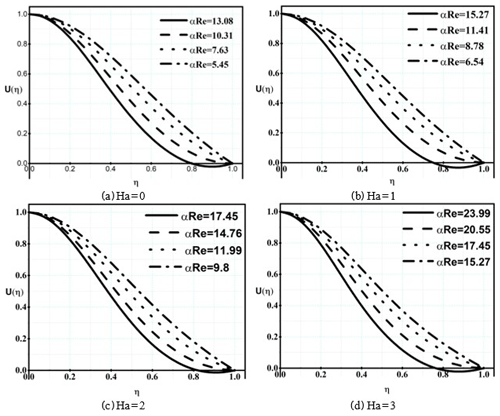
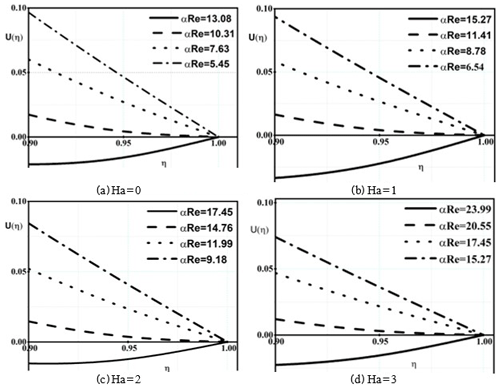
The dimensionless velocity profile for at a certain cross section is shown in Fig. 4. By the magnetic field (Ha) augmentation, αResep. increases; then, for Ha=2, the dimensionless velocity profile becomes tangent. For Ha=0 and Ha=1, there are back flow and for Ha=3 the back flow does not occur.
In Fig. 5, the effect of the magnetic field on the fluid flow regime is demonstrated. As can be seen, for Reα smaller than αResep., the dimensionless velocity vectors are positive directions, which means there is no separation, whereas for the Reα larger than αResep., there is a reverse flow. For example, as is seen in Table 3, the αResep. value corresponding to Ha=2 is 14.76. For αRe=9.18 and αRe=11.99, the dimensionless velocity profile is “normal”, while for αRe=17.45 there is a reverse flow near the wall. In the physical aspect, the dimensionless velocity gradient should be zero on the wall in the separation point. As a validity discussion, it is expected that for a separation point with characteristic αRe=14.76 and Ha=2, the dimensionless velocity profile at η=1 is tangential to the η axis. For the sake of clarity, this along with three other cases are shown in Fig. 6.
In this paper, the separation point displacement for the steady incompressible laminar flow, through a two-dimensional circular diffuser due to the variation of the imposed magnetic field intensity, was investigated. It was concluded that, by increasing the magnetic field intensity, the Lorentz force increases and the separation is delayed. Moreover, in a diffuser of certain conditions, with adjustable magnetic field intensity, one can increase the magnitude of the Lorentz force up to a level that the separation will not occur on the walls.
| umax | Inlet velocity (m s−1) | σ | Electrical conductivity (Ω m)−1 |
| ur | r component of the velocity (m s−1) | J | Density of electric current (A m−2) |
| R | Coordinate in the direction of flow (m) | I | Electric current (A) |
| α | Diffuser half angle (radian) | B | Total magnetic field (T) |
| θ | Angle between center line and wall (radian) | B0 | External magnetic field (T) |
| P | Pressure (Pa) | b | Induced magnetic field (T) |
| Re | Reynolds number | E | Electric field (V m−1) |
| ρ | Density (kg m−3) | Ha | Hartmann number |
| T | Time (s) | Permeability of free space (Tm A−1) | |
| η | Arbitrary variable | μr | Relative permeability |
| U(η) | Dimensionless velocity | μ | Permeability of a specific medium (Tm A−1) |
| f(θ) | A function of θ (m2 s−1) | μ′ | Dynamic viscosity (pa s) |
| ν | Kinematic viscosity (pa s) | (αRe)sep. | Value of αRe at separation point |
All the data used in this paper can be obtained on request from the corresponding author.
MA and SMM proposed the idea and methodology; MKJ, DDG and SMM derived the equations and applied the solution; MA, MKJ and SMM obtained and discussed the results and wrote and revised the manuscript.
The authors declare that they have no conflict of interest.
This paper was edited by Amin Barari and reviewed by three anonymous referees.
Abbasbandy, S. and Shivanian, E.: Exact Analytical Solution of the MHD Jeffery-Hamel flow Problem, Meccanica, 47, 1379–1389, 2012.
Abbasi, M., Ganji, D. D., and Rahni, M. T.: MHD Flow In a Channel Using New Combination Of Order Of Magnitude Technique and HPM, Technical Gazette, 21, 317–321, 2014.
Ahmad, I., Ilyas, H., and Bilal, M.: Numerical Solution for Nonlinear MHD Jeffery-Hamel Blood Flow Problem through Neural Networks Optimized Techniques, J. Appl. Environ. Biol. Sci., 4, 33–43, 2014.
Alam, M. D. S., Khan, M. A. H., and Alim, M. A.: Magnetohydrodynamic Stability of Jeffery-Hamel Flow Using Different Nanoparticles, J. Appl. Fluid Mech., 9, 899–908, 2016.
Ananthaswamy, V. and Yogeswari, N.: A Study on MHD Jeffery-Hamel Flow in Nan-Fluids Using New Homotopy Analysis Method, Int. J. Sci. Res. Modern Ed., 1, 15–28, 2016.
Axford, W. I.: The Magnetohydrodynamic Jeffrey-Hamel Problem For A Weakly Conducting Fluid, J. Mecb. Appl. Math., 14, 335–351, 1961.
Bhatti, M. M., Abbas, M. A., and Rashidi, M. M.: A robust numerical method for solving stagnation point flow over a permeable shrinking sheet under the influence of MHD, Appl. Math. Comput., 316, 381–389, 2018.
Bougoffa, L., Mziou, S., and Rach, R. C.: Exact and Approximate Analytic Solutions of The Jeffery-Hamel Flow Problem by the Duan-Rach Modified Adomian Decomposition Method, Math. Model. Anal., 21, 174–187, 2016.
Davidson, P. A.: An Introduction To Magnetohydrodynamics, Cambridge University Press, 27–60, 2001.
Ellahi, R., Bhatti, M. M., and Pop, I.: Effects of hall and ion slip on MHD peristaltic flow of Jeffrey fluid in a non-uniform rectangular duct, Int. J. Numer. Method. H., 26, 1802–1820, 2016.
Ganji, D. D., Sheikholeslami, M., and Ashorynejad, H. R.: Analytical Approximate Solution of Nonlinear Differential Equation Governing Jeffery-Hamel Flow With High Magnetic Field by Adomian Decomposition Method, International Scholarly Research Network ISRN Mathematical Analysis, 2011, 1–16, 2011.
Ghadikolaei, S., Hosseinzadeh, K., and Ganji, D.: Analysis of unsteady MHD Eyring-Powell squeezing flow in stretching channel with considering thermal radiation and Joule heating effect using AGM, Case studies in thermal engineering, 10, 579–594, 2017.
Hamel, G.: Spiral Formige Bewgungen Zaher Flussigkeiten, Jahresb. Deutsch Math.-Verein, 25, 34–60, 1916.
Hosseinzadeh, K., Amiri, A. J., Ardahaie, S. S., and Ganji, D.: Effect of variable lorentz forces on nanofluid flow in movable parallel plates utilizing analytical method, Case studies in thermal engineering, 10, 595–610, 2017.
Jeffery, G. B.: The Two-Dimensional Steady Motion of a Viscous Fuid, Philos. Mag., 6, 445–465, 1915.
Jhorar, R., Tripathi, D., Bhatti, M., and Ellahi, R.: Electroosmosis modulated biomechanical transport through asymmetric microfluidics channel, Indian J. Phys., 92, 1229–1238, 2018.
Kezzr, M., Sari, M. R., Adjabi, R., and Halahem, A.: A Modified Decomposition Method for Solving Nonlinear Problem of Flow in Converging-Diverging Channel, J. Eng. Sci. Technol.y, 10, 1035–1053, 2015.
Khaki, M., Nejad, M. K., and Ganji, D. D.: New Results for Boundary Layer Flow and Convection Heat Transfer Over a Flat Plate by Using the Homotopy Perturbation Method, Walailak J. Sci. Techol., 11, 325–340, 2014.
Khan, N. A., Sultan, F., Shaikh, A., Ara, A., and Rubbab, Q.: Haar Wavelet Solution of the MHD Jeffery-Hamel Flow and Heat Transfer in Eyring-Powell Fluid, J. Chem. Phys., 6, 109–114, 2016a.
Khan, U., Ahmed, N., Sikandar, W., and Mohyuddin, S. T.: Jeffery Hamel Flow of a Non-Newtonian Fluid, J. Appl. Comput. Mech., 2, 21–28, 2016b.
Makinde, O. D.: Effect of Arbitrary Magnetic Reynolds Number on MHD Flows in Convergent and Divergent Channels, Int. J. Numer. Method. H., 18, 697–707, 2008.
Mirgolbabae, H., Ganji, D. D., Etghani, M. M., and Sobati, A.: Adapt Variational Iteration Method and Axisymmetric Flow Over a Stretching Sheet, World Journal of Modelling and Simulation, 5, 307–314, 2009.
Moakher, P. G., Abbasi, M., and Khaki, M.: Fully Developed Flow of Fourth Grade Fluid through the Channel with Slip Condition in the Presence of a Magnetic Field, J. Appl. Fluid Mech., 9, 2239–2245, 2016.
Moghimi, S. M., Domairry, G., Soleimani, S., and Ghasemi, E. H. B.: Application HAM to Solve MHD Jeffery-Hamel Flows in Non-Parallel Walls, Computers and Mathematics with Applications, 42, 108–113, 2011a.
Moghimi, S. M., Ganji, D. D., Bararnia, H., Hosseini, M., and Jalaal, M.: Homotopy Perturbation Method for Nonlinear MHD Jeffery–Hamel Problem, Computers and Mathematics with Applications, 61, 2213–2216, 2011b.
Regev, O., Umurhan, O. M., and Yecko, P. A.: Modern fluid dynamics for physics and astrophysics, Springer, 56 pp., 2016.
Roidt, M. and Cess, R. D.: An Approximate Analysis of Laminar Magnetohydrodynamic Flow in the Entrance Region of a Flat Duct, J. Appl. Mech., 29, 171–176, 1962.
Sadeghy, K., Khabazi, N., and Taghavi, S.: Magnetohydrodynamic (MHD) Flows of Viscoelastic Fluids in Converging/Diverging Channels, Int. J. Eng. Sci., 45, 923–928, 2007.
Schlichting, H. and Gersten, K.: Boundary Layer Theory, McGraw Hill, 104–109, 2000.
Stow, S. R., Duck, P. W., and Hewitt, R. E.: Three-Dimensional Extensions to Jeffery–Hamel Flow, Fluid Dynam. Res., 29, 25–45, 2001.
Taheri, M. H., Abbasi, M., and Jamei, M. K.: An Integral Method for the Boundary Layer of MHD Non-Newtonian Power-Law Fluid in the Entrance Region of Channels, J. Braz. Soc. Mech. Sci., 39, 4177–4189, 2017.
Vahabzadeh, A., Ganji, D. D., and Abbasi, M.: Analytical Investigation of Porous pin Fins with Variable Section in Fully-Wet Conditions, Case Studies Thermal Engineerin, 5, 12 pp., 2015.
Withe, F. M.: Viscouse Fluid Flow, McGraw-Hill, 161–165, 2006.