the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Buckling of elastically restrained nonlocal carbon nanotubes under concentrated and uniformly distributed axial loads
Mouafo Teifouet Armand Robinson
Buckling of elastically restrained carbon nanotubes is studied subject to a combination of uniformly distributed and concentrated compressive loads. Governing equations are based on the nonlocal model of carbon nanotubes. Weak formulation of the problem is formulated and the Rayleigh quotients are obtained for distributed and concentrated axial loads. Numerical solutions are obtained by Rayleigh–Ritz method using orthogonal Chebyshev polynomials. The method of solution is verified by checking against results available in the literature. The effect of the elastic restraints on the buckling load is studied by counter plots in term of small-scale parameter and the spring constants.
Presently nanoscale components are being used extensively in a variety of nanotechnology applications (Morris and Iniewski, 2013; Tserpes and Silvestre, 2014). In particular, carbon nanotubes (CTN) are used in diverse fields due their superior properties (Endo et al., 2008; Zhang, 2012; Tserpes and Silvestre, 2014) which include high stiffness and low density. To exploit their properties in specific applications, their mechanical behaviour under loading needs to be investigated by mathematical modelling and/or molecular dynamic simulations. The modelling employed in the present study is nonlocal continuum mechanics. Continuum approach in the study of the mechanical behaviour of nano scale structures has been implemented extensively as can be judged from the review articles and the books on the subject (Wang et al., 2010; Eltaher et al., 2016; Kaushik and Majumder, 2015; Rafiei, 2015; Rafii-Tabar et al., 2016). In particular, buckling of carbon nanotubes has been studied extensively by continuum modelling and the recent work on this subject can be found in Reddy (2007), Reddy and Pang (2008), Zhang et al. (2010), Xu et al. (2012), Arash and Wang (2012) and Askari et al. (2017).
Previous studies on the buckling of nanotubes mostly involved rigid boundary conditions such as clamped, hinged and free boundaries. Recent studies on the buckling of nanotubes under a tip load and subject to classical boundary conditions include Ansari et al. (2011), Sahmani and Ansari (2011), Kumar (2016), Kumar and Deol (2016) and Taghizadeh and Ovesy (2016). In these studies the buckling loads for carbon nanotubes were obtained subject to classical boundary conditions. However, elastically restrained boundaries can be observed in a number of applications of nano-scale components. One such application area is nanomechanical sensors (Kiani, 2015) and for sensing nanosized objects (Kiani et al., 2013). Restraints such as rotational springs affect the buckling load that can be carried by a nanotube. Study of the buckling of CTNs subject to elastically restrained end conditions extends the previous results to the cases when the CTN boundaries cannot be modelled simply as hinged, clamped or free boundaries. Previous work on this subject involved the buckling of a nanotube with rotational springs on the boundaries and subject to a concentrated axial load (Wang et al., 2015; Yayli, 2015, 2016).
Present study is directed to determining the stability of carbon nanotubes under compressive axial loads when the nanotube is subject to elastically restrained boundary conditions. Such end conditions arise in situations when the nanotube cannot be attached to the boundaries in a rigid manner. Axial loads are taken as a concentrated tip load and a uniformly distributed axial load which corresponds to buckling under self-weight. Buckling of nanotubes under self-weight has been the subject of studies in Wang et al. (2004), Mustapha and Zhong (2012), Wang et al. (2016). Buckling of nanotubes subject to uniformly and triangularly distributed axial loads has been studied for uniform nanotubes in Robinson and Adali (2016), Robinson et al. (2018) and for non-uniform nanotubes in Robinson and Adali (2017, 2018).
In the present study, the numerical solution of the problem is based on a variational approach involving the weak formulation of the problem incorporating the differential equation and the elastic boundary conditions in a single expression. Rayleigh quotients for the tip load and the distributed axial loads are derived using the weak formulation framework. Rayleigh–Ritz method of solution is implemented via orthogonal Chebyshev polynomials. Solution method is validated by comparing the accuracy of the results with results available in the literature. There have been a number of studies applying Rayleigh–Ritz method to the buckling and vibration of nanotubes (Behera and Chakraverty, 2014; Ghannadpour et al., 2013; Ghannadpour and Mohammadi, 2010, 2011) and the method has been covered extensively in the book by Reddy (2002). Variational formulations for the buckling of nonlocal CTNs have been given in a number of cases (Adali, 2008, 2012).
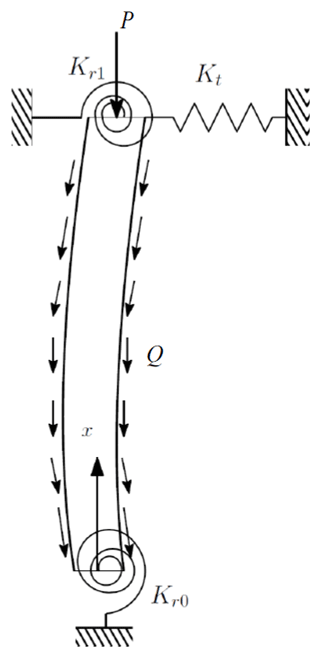
We consider an elastically restrained single-walled carbon nanotube subject to concentrated and uniformly distributed axial loads. The nanotube has length L and the axial load is expressed as
where P is the concentrated axial load applied at the end point x=L and Q is the magnitude of the uniformly distributed axial load as shown in Fig. 1.
The support at x=0 is elastically restrained by a rotational spring with a torsional constant Kr0. The support at x=L is elastically restrained by a rotational spring with a torsional constant Kr1 and a translational spring of constant Kt. The clamped end boundary conditions correspond to Kr0→∞ at x=0 and Kr1→∞ and Kt→∞ at x=L. Simply supported boundary conditions correspond to Kr0=0 at x=0, and Kr1=0 and Kt→∞ at x=L. Free end boundary condition at x=L is given by Kr1=0 and Kt=0. The equation governing the buckling of the elastically restrained column can be expressed in terms of moment M(x) and deflection w(x) as
where x0=0, x1=L and δ(x−xi) is Dirac delta function. The constitutive relation based on the nonlocal theory of elasticity can be expressed as
where η=e0a is the small scale parameter, E is the Young's modulus and I is the moment of inertia. In the expression η=e0a, e0 stands for a constant which is specific to each material. It can be determined either experimentally by using vibration or buckling load measurements or by the use of atomic dispersion relations. The constant a represents an internal characteristics length such as granular distance or lattice parameter. The nonlocal parameter η is also called a small-scale parameter and can be determined by conducting experiments and a comparison of dispersion curves obtained from nonlocal continuum mechanics and molecular dynamics simulations. Generally η≤2 nm for SWCNT and its value depends on many parameters such as boundary conditions, chirality, mode shape, number of walls and type of motion. Further information on the computation and the meaning of η can be found in Challamel et al. (2014) and Wang et al. (2017).
The expression for M(x) is obtained from Eqs. (2) and (3) as
From Eqs. (2) and (4), the differential equation governing the buckling of an elastically restrained nanotube subject to the buckling load N(x) given by Eq. (1) is obtained as
where
Next the weak formulation for Eq. (5) is derived by noting that
The weak formulation of Eq. (5) is a weighted-integral form that incorporates both the governing differential equation and the associated natural boundary conditions. The use of equation Eq. (7) facilitates the derivation of the variational form of the problem as well as the derivation of the boundary conditions as shown below. This approach has been employed in Robinson and Adali (2016, 2017, 2018) for a number of nonlocal buckling problems. Using integration by parts, the following equation can be obtained from Eqs. (5) and (7):
where the boundary terms are given by
with m(xi) and V(xi) denoting the expressions
First the Rayleigh quotient for the concentrated load is derived for the case P>0 and Q=0 (no distributed load). For this case the following relation can be obtained from Eqs. (8), (10) and (11)
The Rayleigh quotient for P (Q=0) follows from Eq. (12) as
Rayleigh quotient for the distributed load Q with no concentrated load applied (P=0) is obtained by a similar computation and the Rayleigh quotient for the case is given by
where
Following dimensionless variables are introduced:
Dimensionless Rayleigh quotient for the case p>0, q=0 can be expressed as
Dimensionless Rayleigh quotient for q>0, p=0 is given by
where
Numerical results are obtained by Rayleigh–Ritz method based on the weak formulation of the problem given in Sect. 3 and the Rayleigh quotients given in Sect. 4. Variational methods of solution of differential equations have been outlined in a number of books (Reddy, 2002; Wunderlich and Pilkey, 2003; Cassel, 2013) and are not detailed here. The essence of the method involves approximating the solution of a differential equation by polynomials using the weak formulation of the problem given by Eq. (8). In the present study, Chebyshev polynomials are employed as the approximating functions expressed as
where r and s take the values 0, 1 or 2 for free, simply supported and clamped boundaries, respectively. Parameters cj are determined as part of the solution of an eigenvalue problem which yields the buckling load as the minimum of the eigenvalues. In Eq. (18), fj(X) is the jth Chebyshev polynomial with f0(X)=1 and f1(X)=X. The remaining terms are obtained from
As noted in Ghannadpour et al. (2013), Chebyshev polynomials provide a set of complete and orthogonal series which leads to rapid convergence as compared to other polynomial series. Furthermore they can be expressed in a relatively simple and uniform form making the coding easier. Fourier series method can also be used effectively as shown in Kadıoglu and Yaylı (2017) where the buckling problem for a nonlocal Timoshenko beam was solved using Fourier series approach.
The polynomial approximation method implemented in the present study to solve the buckling problem for elastically restrained nanotubes is applied to the buckling of elastically restrained columns in order to assess and verify its accuracy. The specific problem involves an elastically restrained column subject to a tip load only, i.e., p>0 and q=0. Numerical results for this problem are given in Wang et al. (2005). Comparative results are given in Table 1 involving a column with a rotational spring constant kr0 at x=0 and a rotational spring constant kr1 at x=L with no translation of the boundary at x=L, i.e., kt=∞. Corresponding results for a column with free end at x=L (kt=0) are given in Table 2. Solutions obtained with the present method are observed to be quite accurate judging from the comparison of the present results with the ones given in Wang et al. (2005) as shown in Tables 1 and 2.
Table 1Critical buckling load p (q=0) for various elastic constraint values with kt=∞ and μ=0 (local column).
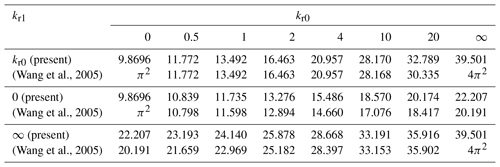
Table 2Critical buckling load p (q=0) for various elastic constraints values with kt=0 and μ=0 (local column).
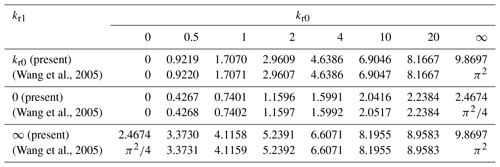
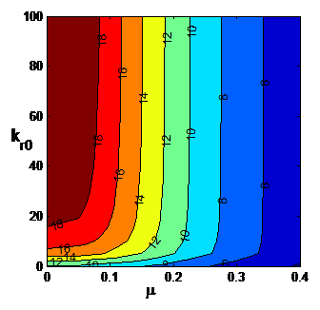
Figure 2Contour plot of the buckling load p (q=0) with respect to μ and kr0 for kr1=0, kt=108 (SS at x=L).
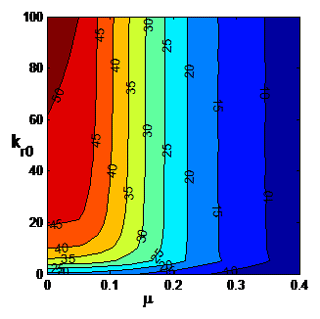
Figure 3Contour plot of the buckling load q (p=0) with respect to μ and kr0 with kr1=0, kt=108 (SS at x=L).
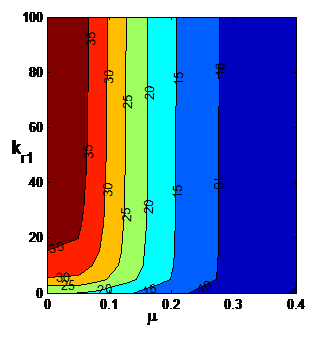
Figure 4Contour plot of the buckling load p (q=0) with respect to μ and kr1 for kr0=108 (clamped at x=0) and kt=108 (no translation at x=L).
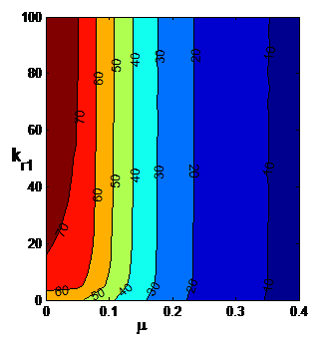
Figure 5Contour plot of the buckling load q (p=0) with respect to μ and kr1 for kr0=108 (clamped at x=0) and kt=108 (no translation at x=L).
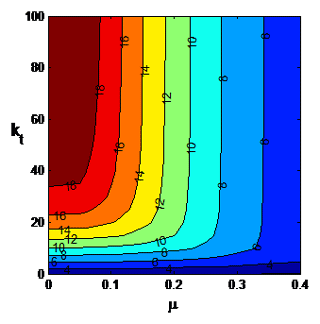
In this section the effect of the elastic restraints on the buckling loads of nonlocal nanotubes is investigated by means of contour plots. Furthermore the buckling loads of nanotubes under a tip load and a distributed load are compared. The numerical results are given in terms of the small scale parameter μ with the range taken as . The contour plots of the buckling load p with respect to μ and kr0 are shown in Fig. 2 for the case kr1=0, kt=108, i.e., the end point x=L is simply supported. It is observed that the buckling load increases as the rotational spring at x=0 becomes stiffer as expected. However this increase becomes minor after a certain value of kr0 depending on the small scale parameter μ. The buckling load increases most as kr0 increases at low values of μ. Increase in the buckling load with increasing kr0 is much less as μ approaches μ=0.4. The corresponding results for uniformly distributed axial load q are shown in Fig. 3. The trends are the same as the concentrated load case shown in Fig. 2. However, the decrease in the buckling load as μ increases is more pronounced.
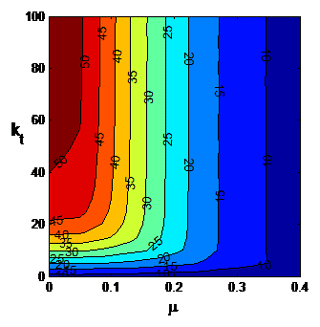
Figure 7Contour plot of the buckling load q (p=0) with respect of kt and μ with kr0=108 (clamped at x=0), kr1=0 (hinge at x=L).
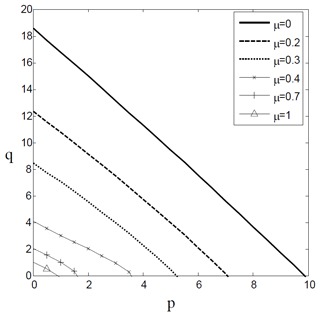
Figure 8Stability boundaries with respect to q and p for kr0=0, kr1=0, kt=108 (SS column) for various values of μ.
Next contour plot of the buckling load under the concentrated load p is shown with respect to μ and kr1 in Fig. 4 for a nanocolumn clamped at x=L. A comparison of Figs. 2 and 4 shows that in this case increase in the buckling load as kr1 increases is more pronounced, but the increase tapers of quickly as μ increases. The corresponding results for uniformly distributed axial load q are shown in Fig. 5 where the increase in the buckling load as kr1 increases is mostly observed for the low values of μ. This increase in the buckling load as kr1 increases is observed to be of minor magnitude. Figure 6 shows the contour plot for the concentrated load p for a clamped-pinned nanocolumn with respect to μ and kt which is the translational spring at x=L. As kt increases, the buckling load p increases substantially for low values of μ with this increase tapering off quickly as μ increases. The corresponding results for uniformly distributed axial load q are shown in Fig. 7 where the increase in q as kt increases is observed to be less pronounced as compared to p. At high values of μ the increase in q is considerably less as kt increases.
Stability boundaries with respect to q and p are shown in Fig. 8 for a simply supported nanocolumn for several values of μ. As expected stability boundary approaches the origin as μ increases.
Buckling of elastically restrained nanotubes subject to concentrated and uniformly distributed axial loads was studied. The elastic restraint at x=0 is specified as a rotational spring and its value changes between a simply supported column (kr0=0) and clamped column (kr0→0). The elastic restraints at x=L are specified as a rotational spring and a translational spring . The value of kr1 changes between a simply supported column (kr1=0) and a clamped column (kr1→∞). Thus the boundary conditions at x=L can vary between a simple support and a clamped support. Numerical results are obtained by Rayleigh–Ritz method employing Chebyshev polynomials of the first kind as the approximating functions. The accuracy of the present method of solution is verified by comparing the numerical results with available results on local columns available in the literature.
The numerical results are given mostly in the form of contour plots to study the effect of the small scale parameter μ and elastic restraints on the buckling loads. It is observed that the effect of the elastic restraints on the buckling load decreases as the small scale parameter increases. Buckling loads are observed to be more sensitive to the changes in the values of the elastic constants when the small-scale parameter is μ≥0.1.
The data was used to generate the graphs in Figs. 2 to 8. Thus these figures contain the data of the present research. The numerical data can be made available upon request from the authors.
MTAR and SA worked on the model jointly and have chosen the Rayleigh-Ritz method and Chebyshev polynomials to obtain the numerical results. MTAR prepared the Figs. 1–8. MTAR and SA contributed to the writing of the article and agreed on the final form of the manuscript.
The authors declare that they have no conflict of interest.
The research reported in this paper was supported by research grants from the University of KwaZulu-Natal (UKZN) and from National Research Foundation (NRF) of South Africa. The authors gratefully acknowledge the supports provided by UKZN and NRF.
This paper was edited by Anders Eriksson and reviewed by Stefan Kaczmarczyk and two anonymous referees.
Adali, S.: Variational principles for multi-walled carbon nanotubes undergoing buckling based on nonlocal elasticity theory, Phys. Lett. A, 372, 5701–5705, https://doi.org/10.1016/j.physleta.2008.07.003, 2008.
Adali, S.: Variational formulation for buckling of multi-walled carbon nanotubes modelled as nonlocal Timoshenko beams, J. Theor. Appl. Mech., 50, 321–333, 2012.
Ansari, R., Sahmani, S., and Rouhi, H.: Rayleigh–Ritz axial buckling analysis of single-walled carbon nanotubes with different boundary conditions, Phys. Lett. A, 375, 1255–1263, https://doi.org/10.1016/j.physleta.2011.01.046, 2011.
Arash, B. and Wang, Q.: A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphenes, Comp. Mater. Sci., 51, 303–313, https://doi.org/10.1016/j.commatsci.2011.07.040, 2012.
Askari, H., Younesian, D., Esmailzadeh, E., and Cveticanin, L.: Nonlocal effect in carbon nanotube resonators: A comprehensive review, Adv. Mech. Eng., 9, 1–24, https://doi.org/10.1177/1687814016686925, 2017.
Behera, L. and Chakraverty, S.: Free vibration of Euler and Timoshenko nanobeams using boundary characteristic orthogonal polynomials, Appl. Nanosci., 4, 347–358, https://doi.org/10.1007/s13204-013-0202-4, 2014.
Cassel, K. W.: Variational Methods with Applications in Science and Engineering, Cambridge University Press, New York, NY, 2013.
Challamel, N., Lerbet, J., Wang, C. M., and Zhang, Z.: Analytical length scale calibration of nonlocal continuum from a microstructured buckling model, Z. Angew. Math. Me., 94, 402–413, https://doi.org/10.1002/zamm.201200130, 2014.
Eltaher, M. A., Khater, M. E., and Emam, S. A.: A review on nonlocal elastic models for bending, buckling, vibrations, and wave propagation of nano scale beams, Appl. Math. Model., 40, 4109–4128, https://doi.org/10.1016/j.apm.2015.11.026, 2016.
Endo, M., Strano, M. S., and Ajayan, P. M.: Potential Applications of Carbon Nanotubes, in: Carbon Nanotubes, Topics Appl. Physics, edited by: Jorio, A., Dresselhaus, G., and Dresselhaus, M. S., Springer-Verlag, Heidelberg, Vol. 111, 13–62, 2008.
Ghannadpour, S. A. M. and Mohammadi, B.: Buckling analysis of micro- and nano-rods/tubes based on nonlocal Timoshenko beam theory using Chebyshev polynomials, Adv. Mater. Res., 123–125, 619–622, https://doi.org/10.4028/www.scientific.net/AMR.123-125.619, 2010.
Ghannadpour, S. A. M. and Mohammadi, B.: Vibration of nonlocal Euler beams using Chebyshev polynomials, Key Eng. Mat., 471, 1016–1021, https://doi.org/10.4028/www.scientific.net/KEM.471-472.1016, 2011.
Ghannadpour, S. A. M., Mohammadi, B., and Fazilati, J.: Bending, buckling and vibration problems of nonlocal Euler beams using Ritz method, Compos. Struct., 96, 584–589, https://doi.org/10.1016/j.compstruct.2012.08.024, 2013.
Kadıoglu, H. G. and Yaylı, M. O.: Buckling analysis of non-local Timoshenko beams by using Fourier series, Int. J. Eng. Appl. Sciences, 9, 89–99, https://doi.org/10.24107/ijeas.362242, 2017.
Kaushik, B. K. and Majumder, M. K.: Carbon Nanotube: Properties and Applications, in: Carbon Nanotube Based VLSI Interconnects, Springer Briefs in Applied Sciences and Technology, https://doi.org/10.1007/978-81-322-2047-3_2, Springer India, New Delhi, 2015.
Kiani, K.: Nanomechanical sensors based on elastically supported double-walled carbon nanotubes, Appl. Math. Comput., 270, 216–241, https://doi.org/10.1016/j.amc.2015.07.114, 2015.
Kiani, K., Ghaffari, H., and Mehri, B.: Application of elastically supported single-walled carbon nanotubes for sensing arbitrarily attached nano-objects, Curr. Appl. Phys., 13, 107–120, https://doi.org/10.1016/j.cap.2012.06.023, 2013.
Kumar, R.: Buckling analysis of single-walled carbon nanotube with nonlocal effect, J. Nanotechn. Applications in Eng., 1, 1–9, 2016.
Kumar, R. and Deol, S.: Nonlocal buckling analysis of single-walled carbon nanotube using differential transform method (DTM), Int. J. Sci. Research, 5, 1768–1773, 2016.
Morris, J. E. and Iniewski, K. (Eds.): Graphene, Carbon Nanotubes, and Nanostructures, CRC Press, Boca Raton, FL, 2013.
Mustapha, K. B. and Zhong, Z. W.: Stability of single-walled carbon nanotubes and single-walled carbon nanocones under self-weight and an axial tip force, Int. J. Eng. Sci., 50, 268–278, https://doi.org/10.1016/j.ijengsci.2010.12.006, 2012.
Rafiei, S.: Foundations of Nanotechnology, Volume 3: Mechanics of Carbon Nanotubes, CRC Press, Boca Raton, FL, 2015.
Rafii-Tabar, H., Ghavanloo, E., and Fazelzadeh, S. A.: Nonlocal continuum-based modeling of mechanical characteristics of nanoscopic structures, Phys. Rep., 638, 1–97, https://doi.org/10.1016/j.physrep.2016.05.003, 2016.
Reddy, J. N.: Energy Principles and Variational Methods in Applied Mechanics, John Wiley & Sons, New Jersey, 2002.
Reddy, J. N.: Nonlocal theory for bending, buckling and vibration of beams, Int. J. Eng. Sci., 45, 288–307, https://doi.org/10.1016/j.ijengsci.2007.04.004, 2007.
Reddy, J. N. and Pang, S. D.: Nonlocal continuum theories of beams for the analysis of carbon nanotubes, J. Appl. Phys., 103, 023511-1-16, https://doi.org/10.1063/1.2833431, 2008.
Robinson, M. T. A. and Adali, S.: Variational solution for buckling of nonlocal carbon nanotubes under uniformly and triangularly distributed axial loads, Compos. Struct., 156, 101–107, https://doi.org/10.1016/j.compstruct.2016.01.026, 2016.
Robinson, M. T. A. and Adali, S.: Buckling of nonuniform carbon nanotubes under concentrated and distributed axial loads, Mech. Sci., 8, 299–305, https://doi.org/10.5194/ms-8-299-2017, 2017.
Robinson, M. T. A. and Adali, S.: Buckling of nonuniform and axially functionally graded nonlocal Timoshenko nanobeams on Winkler-Pasternak foundation, Compos. Struct., 206, 95–103, https://doi.org/10.1016/j.compstruct.2018.07.046, 2018.
Robinson, M. T. A., Kisito, T. P., Laurent, K. Y., and Adali, S.: Analysis of the buckling of carbon nanotube under self-weight: The power series and differential quadrature approaches, Mech. Adv. Mater. Struc., https://doi.org/10.1080/15376494.2018.1430263, online first, 2018.
Sahmani, S. and Ansari, R.: Nonlocal beam models for buckling of nanobeams using state-space method regarding different boundary conditions, J. Mech. Sci. Technol., 25, 2365–2375, 2011.
Taghizadeh, M. and Ovesy, H. R.: Beam Buckling Analysis by Nonlocal Integral Elasticity Finite Element Method, Int. J. Struct. Stab. Dy., 16, 1550015, https://doi.org/10.1142/S0219455415500157, 2016.
Tserpes, K. I. and Silvestre, N. (Eds.): Modeling of Carbon Nanotubes, Graphene and their Composites, Springer International Publishing, Switzerland, 2014.
Wang, C. M., Wang, C. Y., and Reddy, J. N.: Exact Solutions for Buckling of Structural Members, CRC Press, Boca Raton, 2005.
Wang, C. M., Zhang, Y. Y., Xiang, Y., and Reddy, J. N.: Recent studies on buckling of carbon nanotubes, Appl. Mech. Rev., 63, 030804–030818, https://doi.org/10.1115/1.4001936, 2010.
Wang, C. M., Gao, R. P., Zhang, H., and Challamel, N.: Treatment of elastically restrained ends for beam buckling in finite difference, microstructured and nonlocal beam models, Acta Mech., 226, 419–436, https://doi.org/10.1007/s00707-014-1195-0, 2015.
Wang, C. M., Zhang, H., Challamel, N., and Xiang, Y.: Buckling of nonlocal columns with allowance for self-weight, J. Eng. Mech.-ASCE, 142, 04016037-1–04016037-9, https://doi.org/10.1061/(ASCE)EM.1943-7889.0001088, 2016.
Wang, C. M., Zhang, H., Challamel, N., and Duan, W. H.: Eringen's small length scale coefficient for vibration of axially loaded nonlocal Euler beams with elastic end restraints, J. Modeling Mech. Materials, 1, 20160158, https://doi.org/10.1515/jmmm-2016-0158, 2017.
Wang, G. W., Zhao, Y. P., and Yang, G. T.: The stability of a vertical single-walled carbon nanotube under its own weight, Mater. Design, 25, 453–457, https://doi.org/10.1016/j.matdes.2004.01.003, 2004.
Wunderlich, W. and Pilkey, W. D.: Mechanics of Structures Variational and Computational Methods, CRC Press, Boca Raton, 2003.
Xu, S. P., Wang, C. M., and Xu, M. R.: Buckling analysis of shear deformable nanorods within the framework of nonlocal elasticity theory, Physica E, 44, 1380–1385, https://doi.org/10.1016/j.physe.2012.02.022, 2012.
Yayli, M. Ö.: Buckling analysis of a rotationally restrained single walled carbon nanotube, Acta Phys. Pol. A, 127, 678–683, https://doi.org/10.12693/APhysPolA.127.678, 2015.
Yayli, M. Ö.: Buckling analysis of a rotationally restrained single walled carbon nanotube embedded in an elastic medium using nonlocal elasticity, Int. J. Eng. App. Sci., 8, 40–50, https://doi.org/10.24107/ijeas.252144, 2016.
Zhang, Q. (Ed.): Carbon Nanotubes and Their Applications, CRC Press, Boca Raton, FL, 2012.
Zhang, Y. Y., Wang, C. M., and Challamel, N.: Bending, buckling, and vibration of micro/nanobeams by hybrid nonlocal beam model, J. Eng. Mech.-ASCE, 136, 562–574, https://doi.org/10.1061/(ASCE)EM.1943-7889.0000107, 2010.