the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Laparoscope arm automatic positioning for robot-assisted surgery based on reinforcement learning
Lingtao Yu
Xiaoyan Yu
Xiao Chen
Fengfeng Zhang
Compared with the traditional laparoscopic surgery, the preoperative planning of robot-assisted laparoscopic surgery is more complex and essential. Through the analysis of the surgical procedures and surgical environment, the laparoscope arm preoperative planning algorithm based on the artificial pneumoperitoneum model, lesion parametrization model is proposed, which ensures that the laparoscope arm satisfies both the distance principle and the direction principle. The algorithm is divided into two parts, including the optimum incision and the optimum angle of laparoscope entry, which makes the laparoscope provide a reasonable initial visual field. A set of parameters based on the actual situation is given to illustrate the algorithm flow in detail. The preoperative planning algorithm offers significant improvements in planning time and quality for robot-assisted laparoscopic surgery. The improved method which combines the preoperative planning algorithm with deep deterministic policy gradient algorithm is applied to laparoscope arm automatic positioning for the robot-assisted laparoscopic surgery. It takes a fixed-point position and lesion parameters as input, and outputs the optimum incision, the optimum angle and motor movements without kinematics. The proposed algorithm is verified through simulations with a virtual environment built by pyglet. The results validate the correctness, feasibility, and robustness of this approach.
With the development of robotic technology and application of minimally invasive surgery (MIS), the laparoscopic MIS robotic system has been widely used in surgical specialties, such as urology (prostate, bladder and kidney cancer), gynecology (hysterectomy and myomectomy). Compared with traditional laparoscopic surgery, robot-assisted laparoscopic surgery displays high-definition, 3-D image of the lesion to the surgeon via the console and allows the surgeon to perform complex operations by manipulating the master controls. Robot-assisted laparoscopic surgery is more precision, flexibility, and controllable than conventional techniques, so it has become the research hotspot in recent years.
Although robot-assisted surgery has many advantages over traditional surgery, there are also some thorny problems, such as control switching between master controls and robotic arms, real-time synchronization of master-slave position and attitude, MIS robotic system preoperative planning. Besides, reasonable preoperative planning can significantly reduce the operation time; otherwise, it may increase surgical risks.
For MIS robotic system preoperative planning, scholars have proposed many different methods, which are divided into three parts: (1) A heuristic method based on surgeon experience. (2) A method based on the virtual surgical environment. (3) A method based on multi-objective optimization algorithm.
Hanna et al. (1997a) investigated the impact of port placement on endoscopic manipulations, especially knotting. The optimal azimuth and elevation angles were obtained by comparing the execution time and performance quality score of tying a surgeon's knot (Hanna et al., 1997a). Austad et al. (2001) completed the coronary artery bypass grafting procedures on pigs using the Zeus robot-assisted surgical system. The Zeus system configurations, like port placement and pigs' position, were set based on recommendations from hospitals and surgeon experience (Austad et al., 2001). Ferzli and Fingerhut (2004) proposed recommendations of trocar placement for laparoscopic surgery. The abdominal cavity is divided into six parts according to the operation area, and recommendations are given according to different operations and patient posture characteristics (Ferzli and Fingerhut, 2004). Pick et al. (2014) proposed an anatomic guide of port placement for laparoscopic radical prostatectomy, which was performed on the da Vinci robot-assisted surgical system. Compared to traditional port placement, the pubic bone was used as optimal landmark (Pick et al., 2004). Badani et al. (2008) proposed a novel technique of port placement for robotic renal surgery, which aimed to maximize the range of motion and eliminate external collisions (Badani et al., 2008). Cestari et al. (2010) proposed a new method of port placement for laparoscopic radical prostatectomy, which used a nautical inclinometer and a homemade triangle mold (Cestari et al., 2010).
The heuristic method based on the surgeon experience is convenient and practical for the surgeon, so it is widely used in clinical practice. However, this method is related to the surgeon's operating habits and requires extensive surgical experience. More importantly, the advantages of the surgical robot system are not fully developed.
Hayashibe et al. (2005) developed the simulation system for preoperative planning of abdominal surgery. The core of the simulation system was kinematics and haptics; the effectiveness of preoperative planning was validated by the surgeon's evaluation (Hayashibe et al., 2005). Hayashibe et al. (2006) developed a new simulation system with volume rendering of medical images and automatic positioning by kinematics (Hayashibe et al., 2006). Sun et al. (2007) developed a simulator of the da Vinci system, which was mainly used for surgeon training. Its primary functions were the simulation of port placement and the practice of simple surgical operations (Sun et al., 2007). Bauernschmitt et al. (2007) developed a simulator for port placement and enhanced guidance in robot-assisted heart surgery. The simulator was completed off-line, the simulation model is established by using the patient's computed tomography (CT) images to get the best ports position. Through this system, preoperative planning was optimized, the operation time was reduced, and operation quality was improved (Bauernschmitt et al., 2007). Konietschke et al. (2011) developed a simulator of the DLR MiroSurge system, which used the VR-Map device to establish the simulator quickly. Its primary functions were preoperative optimization and intraoperative simulation (Konietschke et al., 2011).
The method based on the virtual surgical environment visualizes the port placement and verifies the effect in advance. Compared with the former method, this method simplifies the steps of port placement and reduces the time required. However, this method also requires surgeons with extensive surgical experience, and due to the lack of analysis of surgical robot performance and finite attempts, it is difficult to obtain optimized preoperative planning.
Sun and Yeung (2007) proposed the selection of optimal port placement and the determination of optimal robot attitude based on multi-objective optimization. This method used two performance indices, the global isotropy index (GII) and the efficiency index (EI). Through the interaction of these two indicators, the flexibility and operability of the robot were improved, and the workspace and visual space were also increased (Sun and Yeung, 2007). Azimian et al. (2010) proposed the preoperative planning method for robot-assisted minimally invasive CABG. This method used sequential quadratic programming to implement the optimization of kinematic and geometric requirements. In the optimization process, individualized preoperative planning can be achieved taking into account the surgeon's experience (Azimian et al., 2010). Ma et al. (2014) proposed the preoperative positioning method, which was mainly aimed at the collision problem of the multi-arm system. It used the maximum distance index to achieve collision-free optimal preoperative positioning (Ma et al., 2014). Yu et al. (2014) proposed the preoperative positioning method, which was mainly aimed at cooperative cooperation between two instrument arms. It used the percentage of collaboration workspace to achieve the optimal cooperation between two manipulators (Yu et al., 2014). Wang et al. (2016) proposed a preoperative planning algorithm for robot-assisted minimally invasive CABG. This algorithm used two performance indices, isotropy index based on CV (IICV) and index of instrument collaboration space (IICS), to implement the optimal port placement selection and the manipulator poses determination (Wang et al., 2016).
Compared with the former two methods, the method based on multi-objective optimization algorithm is more scientific. More importantly, in addition to the surgeon experience, the robot's characteristics are also taken into account, so the preoperative planning is more conducive to the operation.
In general, after obtaining the preoperative planning by the above method, the joint variables of the manipulator are obtained by inverse kinematics. At present, the telecentric fixed-point positioning mechanism of the surgical robot system is mostly an undriven mechanism, which needs to be manually adjusted to the target position. Due to errors of manual adjustment and mechanical kinematics parameters, the actual preoperative planning is not the optimal solution previously determined. Therefore, it is necessary to use a new method to complete preoperative planning instead of manual configuration.
Traditional manipulator control is to calculate joint variables by inverse kinematics of a given target position. At present, its trend has turned to the end-to-end solution. In other words, the controller learns diverse strategies directly from sensors data, rather than relying on fixed strategies such as kinematics (James and Johns, 2016; Otte et al., 2016; Phaniteja et al., 2017; Gu et al., 2017; Mohammadi et al., 2018). James and Johns (2016) proposed a method that took images as its input and outputs motor movements and target position. Thus, the control of the 7-DOF robot arm can be realized in a virtual environment without any prior knowledge (James and Johns, 2016). The telecentric fixed-point positioning mechanism is a redundant mechanism; an accurate kinematic inverse solution can only be obtained under appropriate constraints. In order to improve the effect of preoperative planning, it is necessary to explore a new method to tackle the problems caused by previous methods.
This paper proposes a laparoscope arm preoperative planning algorithm, which is based on the lesion parametrization model and evaluation indexes. Besides, an improved method based on reinforcement learning algorithm is proposed to achieve preoperative laparoscope arm automatic positioning. More importantly, it is a crucial step towards the automation of robot-assisted laparoscopic surgery.
The rest of the paper is organized as follows. Section 2 introduces surgical procedures and MIS robotic system. The laparoscope arm preoperative planning algorithm is introduced in Sect. 3. The improved DDPG algorithm is introduced in Sect. 4. The simulation results are presented in Sect. 5. Discussion and conclusion are given in Sects. 6 and 7, respectively.
2.1 The MIS procedures
The common MIS has three steps: (1) According to the actual surgical needs, a surgeon makes several small incisions (usually 5–15 mm) and inserts a thin tube called trocar. The trocar is deployed as a means of introduction for laparoscope or laparoscopic instruments, like scissors and graspers, to provide an access port during surgery. (2) Creation of a pneumoperitoneum by inflating the abdomen with carbon dioxide to make a separation between organs and increase the operating space of surgical instruments. (3) The surgeon views the magnified image of the patient's internal organs provided by laparoscope on a video monitor. Using different instruments, the surgeon performs a series of surgical operations in the pneumoperitoneum.
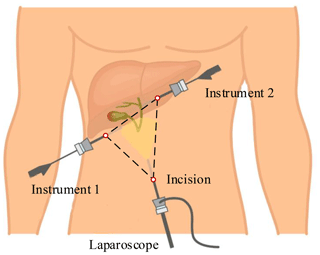
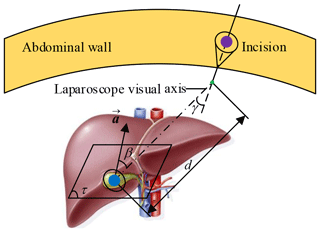
This paper takes laparoscopic cholecystectomy (LC) as an example. The surgeon makes three incisions and inserts trocar. In LC, it is always with the patient in a supine position. Three incisions are arranged in an isosceles triangle for better operating space, as shown in Fig. 1. A laparoscope is placed through a trocar, and specialized instruments are placed through other trocars. By operating the laparoscope and instruments, the surgeon delicately separates the gallbladder from its attachments to the liver and the bile duct and then removes it through one incision.
2.2 Layout design of MIS robotic system
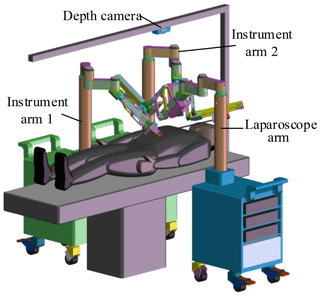
The MIS robotic system includes a master-slave manipulator system and a depth camera. The slave manipulator consists of one laparoscope arm and two instrument arms. Laparoscope arm is equipped with a laparoscope, and instrument arms are equipped with different laparoscopic instruments. Laparoscope arm and instrument arms are located on both sides of the operating bed. A depth camera is installed above the operating bed for acquiring the position of the incisions and robotic arms, as shown in Fig. 2.
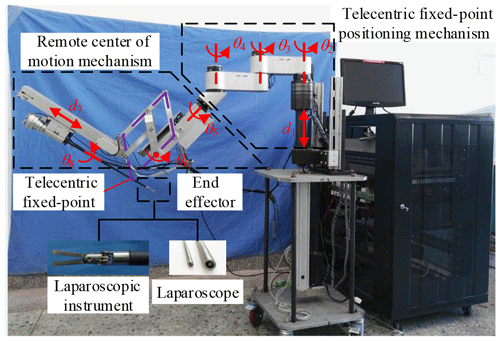
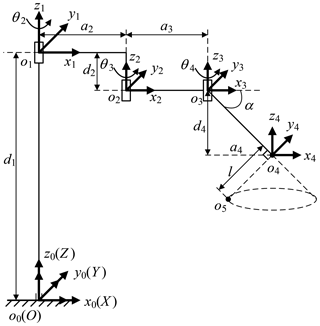
The three arms have the same mechanical structure. Each arm is divided into three parts, the telecentric fixed-point positioning mechanism, the remote center of motion mechanism and the end effector, as shown in Fig. 3. The first part adjusts the spatial position of telecentric fixed-point by three revolving joints and one linear joint. The second part adjusts the position and posture of the end effector by the master manipulator operated by a surgeon; at its end, there is a versatile quick-change mechanism for end effectors installation.
One of the critical issues for MIS is preoperative planning, including preparation for interventions and decision about the optimum surgical incisions. Currently, the surgeon often uses trial-and-error method or experience-based to complete preoperative planning, which may not meet the requirements of the optimum incisions. Therefore, it is necessary to use preoperative planning algorithm instead of the previous method. The preoperative planning includes laparoscope arm and instrument arms preoperative planning. This paper studies the former, including the optimum incision and the optimum angle of laparoscope entry.
3.1 The mathematical model of artificial pneumoperitoneum
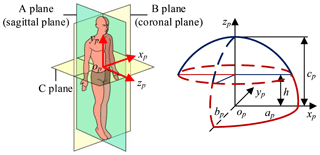
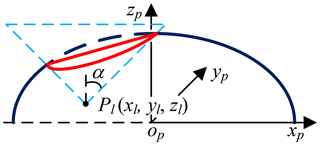
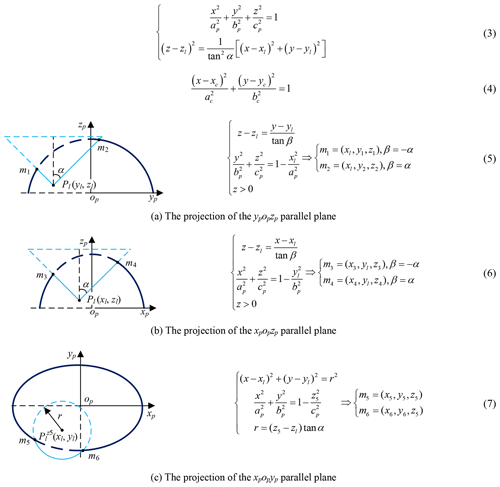
The mathematical model of pneumoperitoneum is established before preoperative planning. The shape of artificial pneumoperitoneum is approximately ellipsoid (Mulier et al., 2008; Oda et al., 2012), so the abdominal wall is simplified to ellipsoid, defined as Eq. (1). The artificial pneumoperitoneal coordinate frame is established by combining the patient's CT images and anatomy. According to anatomy, there are three principal planes, namely the sagittal plane, the coronal plane, and the transverse plane. In the coordinate frame, there are also three reference planes, namely A plane, B plane, and C plane. A plane coincides with the sagittal plane; B plane coincides with the coronal plane; C plane is parallel to the transverse plane, and the pneumoperitoneum is divided equally by C plane. The origin of the coordinate frame is at the intersection of three reference planes. xp-axis is defined along the mediolateral direction; yp-axis is defined along the superior-inferior direction; zp-axis is defined along the anteroposterior direction. In the coordinate frame, the mathematical model of artificial pneumoperitoneum is established, as shown in Fig. 4.
During actual operation, the model parameters (ap, bp, cp) are determined by the medical image and gas insufflation volume. Suppose an adult's chest width is 3.15 dm, chest thickness is 2.45 dm, and chest length is 2.9 dm. The corresponding parameters in Fig. 6 are ap=1.55, bp=1.45, h=1.2 dm. Chen suggested that the gas insufflation volume is about 3L (Chen, 1999). According to Eq. (2), calculate cp=2.27 dm.
3.2 The lesion parametrization model
The surgeon should be clear about the information of the surgical site, including lesion location, lesion anatomy, and surrounding tissues. At present, the conventional method is imaging (radiology) test, and the lesion model and its surrounding environment are obtained by the 3-D reconstruction technology. Describe the relationship between lesion and incision in parametric form, as shown in Fig. 5. Plane τ represents the target operation plane, a represents the normal vector of the plane τ, d represents the distance from the lesion to the laparoscope, β represents the angle between laparoscope visual axis and a, γ represents the laparoscope deviation angle. So, the two principles of laparoscope arm preoperative planning can be expressed as follows: (1) Observation distance principle: laparoscope-to-target distance d=75–150 mm, d≤ the maximum joint variable of d7 (definition in Fig. 3), and no barrier (Hanna et al., 1997b). (2) Observation direction principle: axis-to-target view angle, the smaller β is, the better operative field is. When β=0, the operative field is optimum; in other words, the laparoscope visual axis is perpendicular to the plane τ (Hanna and Cuschieri, 1999).
3.3 The preoperative planning algorithm framework
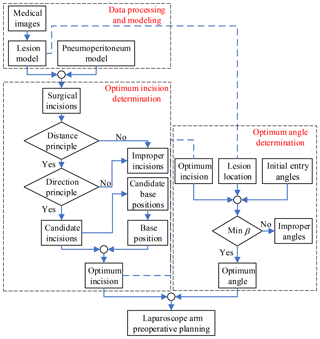
Through the study of the mathematical model of artificial pneumoperitoneum, lesion parametrization model and preoperative planning principles, the laparoscope arm preoperative planning algorithm is proposed, as shown in Fig. 6, that includes three stages: data processing and modeling, optimum incision determination and optimum angle determination.
In the first stage, obtain patient information from the medical images, and then establish the mathematical model of artificial pneumoperitoneum, and lastly determine the location and lesion parametrization model. This stage is the basis of the entire algorithm, and also the most time-consuming stage.
In the second stage, all allowable surgical incisions are obtained from the first stage, and then the candidate incisions are determined according to the two principles. The candidate base positions are obtained by the candidate incisions. According to the actual situation of the operating room, select one of the positions as the base position. Combine candidate incisions and the base position to determine the optimum incision.
In the third stage, the candidate entry angles are determined by combining the optimum incision, lesion location, and initial entry angle. Determine the optimum angle according to the observation direction principle. Since there may be no direction in which the visual axis is perpendicular to the plane τ, the minimum β is chosen as the optimum angle.
Finally, the laparoscope arm preoperative planning algorithm is completed, including the optimum incision and the optimum angle.
3.4 The candidate incisions
The telecentric fixed-point positioning mechanism has four degrees of freedom; the mechanism diagram is shown in Fig. 7. o4 is the telecentric fixed-point, o5 is the end of a laparoscope, and α is determined by the remote center of motion mechanism. The prismatic joint is used to adjust the vertical position of o4, and the three revolute joints are used to adjust the horizontal position. Removing the prismatic joint, it is a planar redundant mechanism. When o4 remains unchanged, the motion trajectory of the laparoscope is a right circular cone with specific apex at o4 and aperture π−2α.
First, candidate incisions are determined based on the distance principle. Assume that the positions of the candidate incision and the lesion are Pi and Pl, respectively. If , Pi satisfies the distance principle. Second, based on the direction principle, the candidate incisions are located on the generatrix of a right circular cone with specific apex at Pl and aperture π−2α. So, candidate incisions are incisions that satisfy the two principles. The following is a mathematical derivation of candidate incisions.
The Pl (xl, yl, zl) is obtained by imaging test; the candidate incisions are located on the intersection (red, Eq. 3) of the abdominal wall (navy blue) and right circular cone with specific apex at Pl (light blue), as shown in Fig. 8. The intersecting line is not a plane curve; it is projected to the plane xpopyp for the convenience of research. The projection curve (Eq. 4) is an ellipse whose expression can be obtained by fitting four points on it. Go through Pl and make two planes parallel to ypopzp and xpopzp, point m1, m2, m3 and m4 are obtained, go through (xl, yl, z5) and make one plane parallel to xpopyp, point m5 and m6 are obtained, as shown in Fig. 9 and Eqs. (5)–(7). The equation's coefficients can be obtained from any four points in the above six points, and the remaining two points are used to verify the correctness of them.
3.5 The candidate base positions
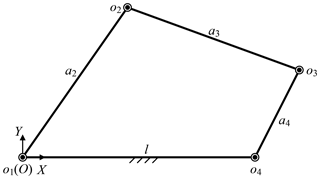
Besides, the base position also affects the surgical incisions. Removing the prismatic joint, the telecentric fixed-point positioning mechanism is a 3-RRR planar redundant mechanism. When o4 remains unchanged, it is simplified as a planar four-bar mechanism, as shown in Fig. 10. In this case, the link length relationship determines whether the laparoscope trajectory is a whole cone, which makes it possible to provide the optimum operative field. In other words, o3o4 should be rotated around o4 while o4 is unchanged, that is, the o3o4 is a crank. Based on the conditions of crank existence, the link length relationship is determined. Assume that the length of link o1o2, o2o3, o3o4 and o4o1 are a2, a3, a4 and l, l determines if there is a crank, which is discussed under three cases, as shown in Eqs. (8)–(10). In summary, the distance from base to fixed-point should be less than to ensure that laparoscope has a complete operative field.
-
The link o1o4 is the longest link:
-
The link o1o4 is the shortest link:
-
The link o1o4 is neither the longest nor the shortest link:
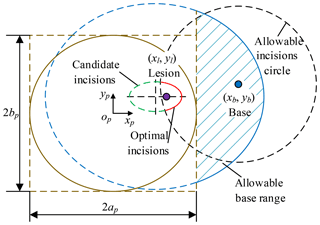
According to Sect. 3.4, the allowable base range is an ellipse. Compared with the projection of the candidate incisions on the plane xpopyp, the center coordinate is unchanged and the semi-major axis and semi-minor axis increase lmax. The intersection of allowable base range and non-interference area in the operating room is the candidate base positions, as shown in Eq. (6).
3.6 The optimum incision and the optimum angle
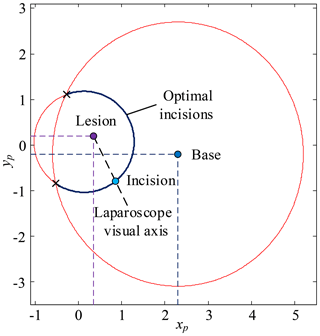
Pb (xb, yb, zb) is chosen as the base position, so the optimum incisions are within allowable incisions circle with the Pb as the origin and lmax as the radius. The optimum incisions (red) are located on the intersection of candidate incisions (green) and allowable incisions circle (black), as shown in Fig. 11 and Eq. (7). The optimum angle of laparoscope entry is β=0, that is, laparoscope visual line coincides with the line relating incision to the lesion. To sum up, combined with Sects. 3.5 and 3.6, the laparoscope arm preoperative planning algorithm is completed.
Given a set of parameters based on the actual situation, the steps of the algorithm are described in detail, a2=220 mm, a3=220 mm, a4=150 mm, α=45∘, , (in the op−xpypzp coordinate frame).
3.6.1 Step 1 Determine candidate incisions
Take the data in Sect. 3.1, mm, d(PiPl)max=sqrt (h2+(ap ( mm (sqrt = square root), the result shows that any point on the abdominal wall can be used as a candidate incision. The candidate incisions are located on the curve, as shown in Eq. (13). According to Sect. 3.4, the projection of the curve on the plane xpopyp is shown in Eq. (14).
3.6.2 Step 2 Determine base position
The candidate base positions are located on the curve, as shown in Eq. (8). Within the allowable base range, choose a base position , zb), zb is determined according to the condition of the operating room.
3.6.3 Step 3 Determine the optimum incision and the optimum angle
First, determine xi based on the surgical needs, body condition and surgeon's operating habits, calculate yi based on Eq. (9), calculate zi based on the mathematical model of pneumoperitoneum, the optimum incision is (xi, yi, zi). Second, the optimum visual axis direction is the line connecting the optimum incision to the lesion. The optimum incision and optimum angle are shown in Fig. 12.
4.1 Problem description
Reinforcement learning describes the set of learning problems where an agent should learn how to map states to actions in an environment to maximize the defined reward function. Throughout the learning process, an agent is not told which actions to take but instead should find out which action yield the most reward by trying various actions. In most cases, actions may affect not only the immediate reward but also the next state, and through that all subsequent rewards. In solving practical problems, it should define a reasonable reward function to compute the reward for taking actions and have a goal relating to the state of the environment. Also, it should quantify all the variables the environment describes and have access to these variables at each step or state.
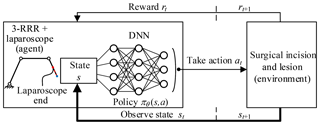
In this paper, the agent is the 3-RRR planar redundant mechanism which is a simplified model of telecentric fixed-point positioning mechanism plus laparoscope. The environment is the lesion and the surgical incision obtained through the preoperative planning algorithm. The actions are the movement of three revolute joints. The agent–environment interaction is shown in Fig. 13.
4.2 Deep deterministic policy gradient (DDPG)
In this paper, laparoscope arm automatic positioning is achieved by DDPG, which is a model-free, off-policy actor-critic algorithm based on the deterministic policy gradient (DPG) (Silver et al., 2014). Deep neural network (DNN) function approximators were used to estimate the action-value function. Thus, the algorithm can learn policies in high-dimensional, continuous action spaces.
Based on DPG, DDPG combines the ideas underlying the success of Deep Q Network (DQN) (Mnih et al., 2013, 2015). It can learn value functions stably and robustly due to two aspects. First, the network is trained off-policy with samples from a replay buffer to minimize correlations between samples. Second, the network is trained with a target Q network to give consistent targets during temporal difference backups. Meanwhile, batch normalization is used to accelerate deep network training and improve the accuracy of the model (Ioffe and Szegedy, 2015).
DDPG contains a parameterized actor function μ(s|θμ) and critic network Q(s, a|θQ) with weights θμ and θQ. The critic network is learned using the Bellman equation (Eqs. 10–10) to make the L(θQ) smaller and smaller. In other words, Q(s, a|θQ) gets closer to the actual value.
where
The actor function is updated by the chain rule (Eq. 11) to the expected return from the start distribution J with respect to the actor parameters.
Every n steps DDPG updates the target networks of actor and critic using “soft” target updates (Eq. 12), rather than directly copying the weights.
4.3 Reward function construction
In the training process, telecentric fixed-point (marked point) position and lesion location are taken as the input of the DDPG algorithm. The fixed-point is obtained by a depth camera, the optimum incision, the optimum angle and the base position are obtained by the preoperative planning algorithm. The DDPG algorithm that combines the algorithm can learn policies directly from the inputs, to achieve laparoscope arm automatic positioning for the robot-assisted laparoscopic surgery. The reward function is essential for the algorithm to learn policies successfully. It consists of intermediate reward and final reward, where the former is given a continuous, guided negative reward when the task is not completed, and the latter is given a positive reward that is one to two orders of magnitude larger than the former when the task is completed. The continuous reward function can make convergence of the algorithm better.
In the op−xpypzp coordinate frame, the fixed-point position is Pf (xf, yf, zf), the incision position is Pi (xi, yi, zi), the laparoscope end position is Pe (xe, ye, ze), and the lesion location is Pl (xl, yl, zl). The goal of the task is 0 (lsinα (definition in Fig. 7) is equal to for programming convenience.). The intermediate reward is ) and is normalized to [] interval. The final reward is 10.
4.4 States description
To improve the convergence of the algorithm, the state variables also play a crucial role in addition to the reward function. If state variables can adequately present the environment, the algorithm can learn policies quickly. Because the image from the depth camera contains all the state information of the environment, it is reasonable to use the image directly as input. However, due to the limitations of the hardware, the processing image data is very slow. To speed up training of the algorithm, it uses a low-dimensional states description, such as joint variables and positions, instead of high-dimensional renderings of the environment.
The algorithm is to make the laparoscope arm move to the target position, so the joint variables are used as the state variables. However, from the training results, these variables cannot adequately describe the environment; in other words, the algorithm cannot achieve the laparoscope arm automatic movement. So, the distance from telecentric fixed-point to incision, the distance from laparoscope end to the lesion, and whether the target is reached are added to the state variables. The experimental results of these two state variables are described in Sect. 5.2.
5.1 Simulation details
The environment is simulated using Pyglet, including a lesion point, a surgical incision and a simplified model of the telecentric fixed-point positioning mechanism. For this environment, a lesion point is randomly specified within a reasonable range, an incision and a base location are obtained by the preoperative planning algorithm. Batch normalization is used on the state input, all layers of the actor network and all layers of the critic network before the action input. In this way, it can learn effectively across tasks with different types of units, without needing to ensure the units are within a set range manually.
TensorFlow is used in the code for high-performance numerical computation. The simulations use Adam (Kingma and Ba, 2015) for learning neural network parameters with a learning rate of 10−5 for the actor and critic. For Q it includes L1 weight decay of 0.1, L2 weight decay of 10−3 and a discount factor of γ=0.9. For the soft target updates, it uses τ=0.01. The neural networks use the rectified non-linearity for all hidden layers (Glorot et al., 2011). The networks have three hidden layers with 900, 900 and 60 units respectively, and the final output layer of the actor is a tanh layer, to bound the actions. The actions are not included until the 3rd hidden layer of Q. The layers weights and biases of both the actor and critic are initialized from a uniform distribution [−x, x], where x=sqrt (6./(in + out)). It trains with minibatch sizes of 16, and it uses a replay buffer size of 6×104. The behavior policy during training is ε-greedy with ε annealed linearly from 1 to 0.1 over the first hundred episodes and fixed at 0.1 after that. The simulations train for a total of 2000 episodes; every episode is terminated if the goal is not completed after 600 steps.
5.2 Simulation results
Two simulations are set up to evaluate the performance of the improved method applied to laparoscope arm automatic positioning for the robot-assisted laparoscopic surgery. The two simulations make one change to states description during training only, and use the same network architecture, learning algorithm and hyperparameters settings. States descriptor one is three joint variables and states descriptor two is the former plus the distance from fixed-point to incision, the distance from laparoscope end to the lesion, and whether the target is reached.
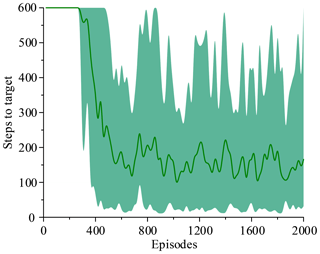
The two simulations evaluate the policy periodically during training by testing it without exploration noise. The improved method with 3 action dimensions and 20 state dimensions runs ten times in the simulated environment. Performance after training across the environment for at most 2000 episodes. The results of ten training sessions report both total reward per episode and steps to target, as shown in Figs. 14–17. The solid line in the figure represents the average over ten sessions, the upper boundary of the shadow part represents the maximum over ten sessions, and the lower boundary represents the minimum value.
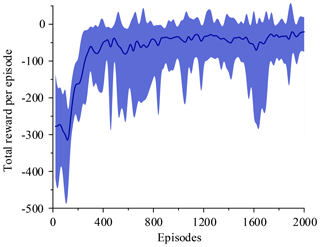
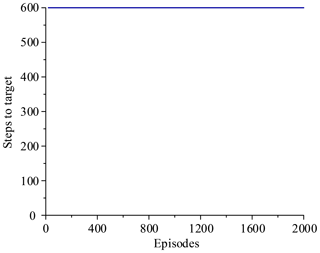
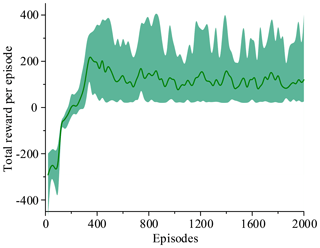
Figure 14 shows that the average of total reward per episode is stabilized to negative and only a few episodes total reward are positive. Figure 15 shows that the steps to target are always 600. These two figures show that it never reaches the goal. Figure 16 shows that the average of total reward per episode increases from −300 to about 120. After 400 episodes, the total reward converges to around 120. Figure 17 shows the steps to target stabilizes at about 150. These two figures show that it reaches the goal after 400 episodes. The results illustrate the states descriptor two is outperformed states descriptor one, the latter does not enable the agent to converge to a good solution, but the former can do it. In other words, the improved method which uses the states descriptor two can learn the right policies on laparoscope arm automatic positioning.
The preoperative planning algorithm, based on the artificial pneumoperitoneum model and the lesion parametrization model, appears to offer significant improvements in planning time and quality for robot-assisted laparoscopic surgery over experience-based method or literature-based method. The distance principle and the direction principle ensure that the proposed algorithm can meet the surgeon's surgical requirements. Furthermore, preoperative planning does not require an additional landmark on the abdominal wall or particular patient positioning.
The proposed algorithm is designed to simulate the actual clinical procedure of robot-assisted surgery or applied to a virtual surgery training system, and a standardized procedure is proposed for preoperative planning. By taking LC as an example, the results indicate that the port placement and laparoscope entry angle selection have satisfying performance, especially for less experienced surgeons.
Preoperative laparoscope arm automatic positioning is achieved based on the DDPG. In this algorithm, the states descriptor plays a crucial role and affects the performance of the algorithm. From the results, the states descriptor two is outperformed states descriptor one. Although the controller does not learn a reasonable strategy directly from states descriptor one, with the evolution of episodes, the controller still improves compared to the initial. Therefore, it is crucial to select states descriptor reasonably. The controller learns a reasonable strategy from states descriptor two, but there is room to reduce the steps of the target, to improve the learning efficiency of the controller. Furthermore, the laparoscope arm automatic positioning is independent of robot configuration and can be extended to any surgical robot system.
This method successfully learns a controller in simulation, and the next step is to study to learn a controller in real robots without a lot of time training, and the method can be extended to the preoperative planning of other operations or even other surgical procedures. Thus, the implementation of the algorithm for robot-assisted surgery can further realize telesurgery, thereby improving the medical level in many areas.
This paper completes the preoperative planning by analyzing the surgical procedures and surgical environment of robot-assisted laparoscopic surgery. Based on the lesion parametrization model, two principles of laparoscope arm preoperative planning are designed, including the distance principle and the direction principle. According to the two principles, the laparoscope arm preoperative planning algorithm is divided into two parts, the optimum incision and the optimum angle of laparoscope entry. A set of parameters based on the actual situation is given to verify the effectiveness of the algorithm. Preoperative laparoscope arm automatic positioning is achieved by the improved method which combines the preoperative planning algorithm with the DDPG algorithm. The improved method takes the fixed-point position captured by a depth camera and the lesion location obtained by imaging test as input. Based on the input information, optimum incision and optimum angle are obtained through the algorithm, and then the laparoscope arm can automatically move to the target position. Compared to the traditional method, kinematics is not used to calculate the motor movements, so that it can reduce errors caused by inaccuracy of kinematic parameters and improve the effectiveness of preoperative planning. The simulation results show that the improved method can realize preoperative laparoscope arm automatic positioning and it is also robust.
The automatic positioning algorithm provides a theoretical basis for the laparoscope arm preoperative planning of robot-assisted laparoscopic surgery. It avoids the disadvantage of the heuristic method based on surgeon experience, and it also simplifies the preoperative planning process and reduces the operation time. However, the algorithm is implemented in a virtual environment, and there is a certain gap with the actual system. Therefore, how to implement the algorithm in the actual system is the primary direction of subsequent research.
The data in this study can be requested from the corresponding author.
LY, XY, XC and FZ discussed and decided on the methodology in the study. The preoperative planning algorithm, the reinforcement learning algorithm and simulations have been performed by XY, XC and FZ. LY completed literature review and overall plan.
The authors declare that they have no conflict of interest.
The paper is supported by the Natural Science Foundation of Heilongjiang Province (Grand No. F2015034). We also greatly appreciate the efforts of the reviewers and our colleagues.
This paper was edited by Jinguo Liu and reviewed by Yi Yang and two anonymous referees.
Austad, A., Elle, O. J., and Røtnes, J. S.: Computer-aided planning of trocar placement and robot settings in robot-assisted surgery, Int. Congr. Series, 1230, 1020–1026, https://doi.org/10.1016/S0531-5131(01)00179-0, 2001.
Azimian, H., Breetzke, J., Trejos, A. L., Patel, R. V., Naish, M. D., Peters, T., Moore, J., Wedlake, C., and Kiaii, B.: Preoperative planning of robotics-assisted minimally invasive coronary artery bypass grafting, in: 2010 IEEE International Conference on Robotics and Automation, Anchorage, United States, 3–7 May 2010, 1548–1553, 2010.
Badani, K. K., Muhletaler, F., Fumo, M., Kaul, S., Peabody, J. O., Bhandari, M., and Menon, M.: Optimizing robotic renal surgery: the lateral camera port placement technique and current results, J. Endourol., 22, 507–510, https://doi.org/10.1089/end.2007.0228, 2008.
Bauernschmitt, R., Feuerstein, M., Traub, J., Schirmbeck, E. U., Klinker, G., and Lange, R.: Optimal port placement and enhanced guidance in robotically assisted cardiac surgery, Surg. Endosc., 21, 684–687, https://doi.org/10.1007/s00464-006-9057-z, 2007.
Cestari, A., Buffi, N. M., Scapaticci, E., Lughezzani, G., Salonia, A., Briganti, A., Rigatti, P., Montorsi, F., and Guazzoni, G.: Simplifying patient positioning and port placement during robotic-assisted laparoscopic prostatectomy, Eur. Urol., 57, 530–533, https://doi.org/10.1016/j.eururo.2009.11.028, 2010.
Chen, X. R.: How to establish pneumoperitoneum safely in laparoscopic surgery, J. Abdomin. Surg., 12, 12–13, https://doi.org/10.3969/j.issn.1003-5591.1999.01.006, 1999.
Ferzli, G. S. and Fingerhut, A.: Trocar placement for laparoscopic abdominal procedures: a simple standardized method, J. Am. Coll. Surgeons, 198, 163–173, https://doi.org/10.1016/j.jamcollsurg.2003.08.010, 2004.
Glorot, X., Bordes, A., and Bengio, Y.: Domain adaptation for large-scale sentiment classification: A deep learning approach, in: ICML'11 Proceedings of the 28th International Conference on International Conference on Machine Learning, Bellevue, United States, 28 June–2 July 2011, 513–520, 2011.
Gu, S., Holly, E., Lillicrap, T., and Levine, S.: Deep reinforcement learning for robotic manipulation with asynchronous off-policy updates, in: 2017 IEEE International Conference on Robotics and Automation, Singapore, Singapore, 29 May–3 June 2017, 3389–3396, 2017.
Hanna, G. and Cuschieri, A.: Influence of the optical axis-to-target view angle on endoscopic task performance, Surg. Endosc., 13, 371–375, https://doi.org/10.1007/s004649900992, 1999.
Hanna, G., Shimi, S., and Cuschieri, A.: Optimal port locations for endoscopic intracorporeal knotting, Surg. Endosc., 11, 397–401, https://doi.org/10.1007/s004649900374, 1997a.
Hanna, G., Shimi, S., and Cuschieri, A.: Influence of direction of view, target-to-endoscope distance and manipulation angle on endoscopic knot tying, Brit. J. Surg., 84, 1460–1464, https://doi.org/10.1111/j.1365-2168.1997.02835.x, 1997b.
Hayashibe, M., Suzuki, N., Hashizume, M., Kakeji, Y., Konishi, K., Suzuki, S., and Hattori, A.: Preoperative planning system for surgical robotics setup with kinematics and haptics, The Int. J. Med. Robot. Comput. Assist. Surg., 1, 76–85, https://doi.org/10.1002/rcs.18, 2005.
Hayashibe, M., Suzuki, N., Hashizume, M., Konishi, K., and Hattori, A.: Robotic surgery setup simulation with the integration of inverse-kinematics computation and medical imaging, Comput. Methods Progr. Biomed., 83, 63–72, https://doi.org/10.1016/j.cmpb.2006.04.010, 2006.
Ioffe, S. and Szegedy, C.: Batch normalization: accelerating deep network training by reducing internal covariate shift, arXiv preprint, arXiv:1502.03167, 2015.
James, S. and Johns, E.: 3D simulation for robot arm control with deep Q-learning, arXiv preprint, arXiv:1609.03759, 2016.
Kingma, D. P. and Ba, L. J.: Adam: A method for stochastic optimization. in: International Conference on Learning Representations 2015, San Diego, United States, 7–9 May 2015, 1–15, 2015.
Konietschke, R., Bodenmüller, T., Rink, C., Schwier, A., Bäuml, B., and Hirzinger, G.: Optimal setup of the DLR MiroSurge telerobotic system for minimally invasive surgery, in: 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011, 3435–3436, 2011.
Ma, R. Q., Wang, W. D., Dong, W., and Du, Z. J.: Preoperative positioning analysis of the celiac minimally invasive surgery robotic system based on an improved gradient projection algorithm, Robot, 32, 156–163, 2014.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., and Riedmiller, M.: Playing atari with deep reinforcement learning, arXiv preprint, arXiv:1312.5602, 2013.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., Graves, A., Riedmiller, M., Fidjeland, A. K., Ostrovski, G., Petersen, S., Beattie, C., Sadik, A., Antonoglou, I., King, H., Kumaran, D., Wierstra, D., Legg, S., and Hassabis, D.: Human-level control through deep reinforcement learning, Nature, 518, 529–533, https://doi.org/10.1038/nature14236, 2015.
Mohammadi, B., Kerzel, M., Görner, M., Zamani, M. A., Eppe, M., and Wermter. S.: Neural end-to-end learning of reach for grasp ability with a 6-dof robot arm, in: Workshop on Machine Learning in Robot Motion Planning–2018 IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018, 1–3, 2018.
Mulier, J., Coenegrachts, K., and Moortele, K. V. D.: CT analysis of the elastic deformation and elongation of the abdominal wall during colon inflation for virtual coloscopy, Eur. J. Anaesthesiol., 25, 42, https://doi.org/10.1097/00003643-200805001-00132, 2008.
Oda, M., Qu, J. D., Nimura, Y., Kitasaka, T., Misawa, K., and Mori, K.: Evaluation of deformation accuracy of a virtual pneumoperitoneum method based on clinical trials for patient-specific laparoscopic surgery simulator, Medical Imaging 2012: Image-Guided Procedures, Robotic Interventions, and Modeling, 8316, 8316G, https://doi.org/10.1117/12.911701, 2012.
Otte, S., Zwiener, A., Hanten, R., and Zell, A.: Inverse recurrent models–an application scenario for many-joint robot arm control, in: Artificial Neural Networks and Machine Learning–International Conference on Artificial Neural Networks 2016, Barcelona, Spain, 6–9 September 2016, 149–157, 2016.
Phaniteja, S., Dewangan, P., Guhan, P., Sarkar, A., and Krishna, K. M.: A deep reinforcement learning approach for dynamically stable inverse kinematics of humanoid robots, in: 2017 IEEE International Conference on Robotics and Biomimetics, Macau, China, 5–8 December 2017, 1818–1823, 2017.
Pick, D. L., Lee, D. I., Skarecky, D. W., and Ahlering, T. E.: Anatomic guide for port placement for daVinci robotic radical prostatectomy, J. Endourol., 18, 572–575, https://doi.org/10.1089/end.2004.18.572, 2004.
Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D., and Riedmiller, M.: Deterministic policy gradient algorithms, in: ICML'14 Proceedings of the 31st International Conference on International Conference on Machine Learning, Beijing, China, 21–26 June 2014, 387–395, 2014.
Sun, L. W. and Yeung, C. K.: Port placement and pose selection of the da Vinci surgical system for collision-free intervention based on performance optimization, in: 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, United States, 29 October–2 November 2007, 1951–1956, 2007.
Sun, L. W., Meer, F. V., Schmid, J., Bailly, Y., Thakre, A. A., and Yeung, C. K.: Advanced da Vinci surgical system simulator for surgeon training and operation planning, The Int. J. Med. Robot. Comput. Assist. Surg., 3, 245–251, https://doi.org/10.1002/rcs.139, 2007.
Wang, W., Wang, W. D., Dong, W., Du, Z. J., and Sun, Y. P.: A preoperative planning algorithm based on dexterity and collaborationspace for the robot-assisted minimally invasive surgery, Robot, 38, 208–216, https://doi.org/10.13973/j.cnki.robot.2016.0208, 2016.
Yu, L. T., Wang, Z. Y., Sun, L. Q., Wang, W. J., and Wang, L.: Research on preoperative positioning analysis of instrument arms for minimally invasive surgical robot, in: 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014, 1269–1275, 2014.